Symétries par rapport à un plan : cas de deux segments (2)
Partie
Question
Dans un repère orthonormé direct \(\mathcal{R} = (O ; x , y , z)\), on considère deux points \(A\) et \(B\) symétriques par rapport au plan \(xOy\).
Le segment \(AO\) est parcouru par un courant d'intensité \(I\) allant de \(A\) vers \(O\).
Le segment \(OB\) est parcouru par le même courant \(I\) allant de \(O\) vers \(B\).
Que peut-on conclure sur la direction du champ magnétostatique \(\vec B\) en un point \(M\) du plan \(xOy\) à partir de la théorie des symétries ?
Aide simple
On représente le cas traité sur la figure suivante :
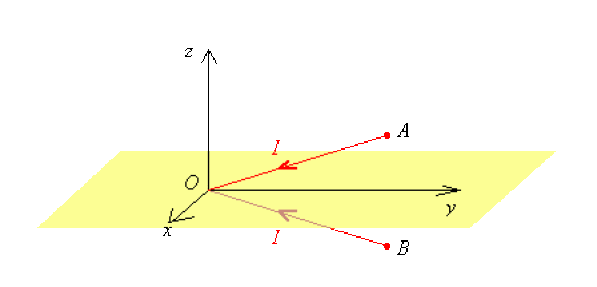
Le plan \(xOy\) est-il alors un plan de symétrie ou d'antisymétrie pour la distribution de courant ?
Solution détaillée
On constate que le plan \(xOy\) est un plan d'antisymétrie pour la distribution de courant.
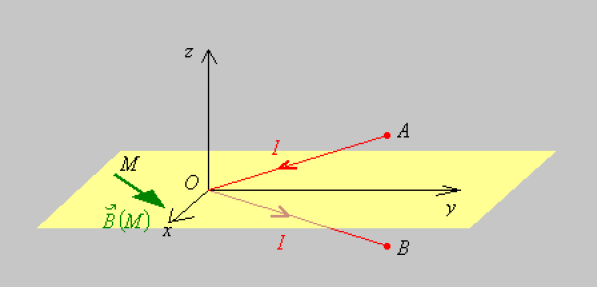
\(\vec B(M)\), qui est un pseudo-vecteur (vecteur axial), est contenu dans les plans d'antisymétrie de la distribution de courant.
Ainsi, pour tous les points \(M\) du plan \(xOy\), le champ magnétostatique \(\vec B(M)\) est contenu dans ce plan.