Symétries par rapport à un plan : cas d'une spire carrée
Partie
Question
On considère une spire carrée \(ABCD\). Elle est parcourue par un courant d'intensité \(I\), dont le sens est donné sur la figure ci-dessous.
Le plan \(\pi\) est orthogonal à \(AB\) et \(CD\), il coupe la spire en deux parties égales.
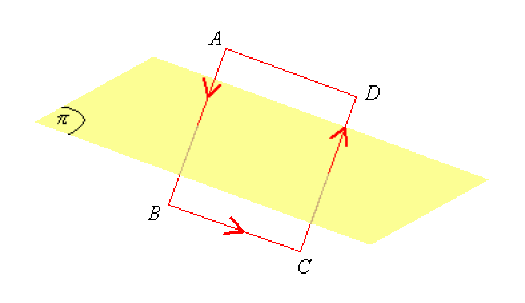
Soit \(M\) un point de ce plan, que peut-on dire de \(\vec B(M)\) en exploitant les symétries de la distribution de courant ?
Aide simple
En considérant successivement les segments \(AB\), \(CD\) puis \(AD\) et \(BC\), peut-on conclure que le plan \(\pi\) est un plan d'antisymétrie ?
Solution détaillée
Le plan \(\pi\) est un plan d'antisymétrie pour le segment \(AB\).
Le plan \(\pi\) est un plan d'antisymétrie pour le segment \(CD\).
Le plan \(\pi\) est un plan d'antisymétrie pour l'association des segments \(AD\) et \(BC\).
C'est donc un plan d'antisymétrie pour l'ensemble de la distribution de courant (conclusion que l'on aurait pu citer sans justification).
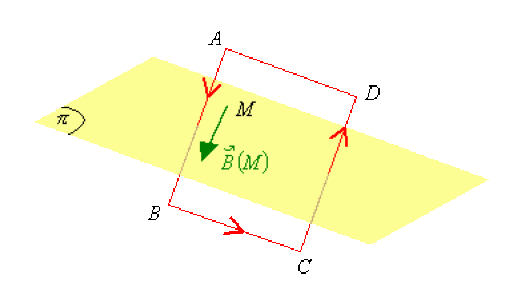
\(\vec B(M)\), qui est un pseudo-vecteur (vecteur axial), est contenu dans les plans d'antisymétrie pour la distribution de courant.
Pour tous les points \(M\) du plan \(\pi\), le champ magnétostatique \(\vec B(M)\) est alors contenu dans ce plan.