Symétries par rapport à un plan : cas de deux spires circulaires
Partie
Question
On considère deux spires circulaires superposables et d'axe commun. Soit \(\pi\) le plan médiateur du segment qui joint leurs centres, lui-même parallèle aux plans des spires.
Elles sont parcourues par des courants d'intensités égales \(I\), orientés comme indiqué sur la figure ci-dessous :
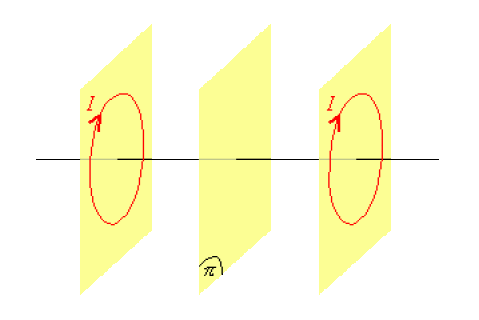
Soit \(M\) un point appartenant au plan \(\pi\), que peut-on dire du champ magnétostatique \(\vec B(M)\) créé par les spires en \(M\) ?
Aide simple
Le plan \(\pi\) est-il un plan de symétrie pour la distribution de courant ?
Solution détaillée
Le plan \(\pi\) est un plan de symétrie pour la distribution de courant.
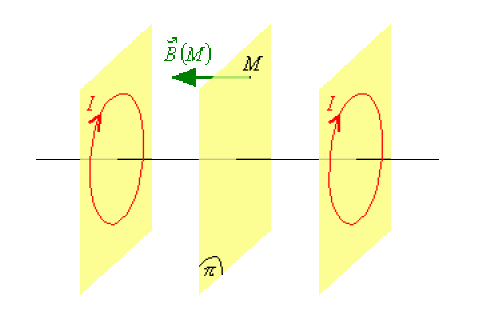
\(\vec B\), qui est un pseudo-vecteur (vecteur axial), est perpendiculaire à tout plan de symétrie pour la distribution de courant.
Pour tous les points \(M\) du plan \(\pi\), le champ magnétostatique \(\vec B(M)\) est perpendiculaire à ce plan.