Champ élémentaire créé par une demi-spire circulaire
Durée : 12 mn
Note maximale : 5
Question
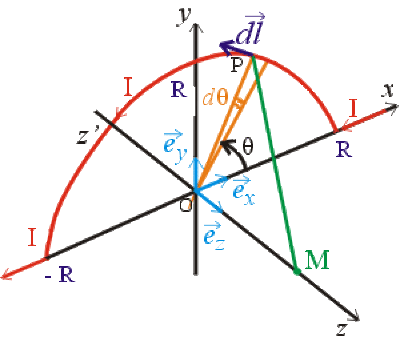
On considère dans un repère \(\mathfrak{R}(O; x,y,z)\), un demi cercle de centre \(O\), de rayon \(R\), d'axe \(z'z\), situé dans le plan \(Oxy\) et parcouru par un courant continu d'intensité \(I\).
Exprimer le champ élémentaire \(d\vec B(M)\) crée par l'élément de courant \(Idl\) centré en un point \(P\) de la demi spire, au point \(M\) de \(z'z\) en fonction de \(I\), \(R\), \(z\), \(dl\) et \(PM\).
Exprimer les composantes de \(PM\) et de dl dans la base \((\vec{e_x}, \vec{e_y}, \vec{e_z})\).
Exprimer \(d\vec B(M)\) dans la base \((\vec{e_x}, \vec{e_y}, \vec{e_z})\).
Solution
\(d\vec B(M)=\frac{\mu_0I}{4\pi}\vec{dl}\wedge\frac{\vec{PM}}{PM^3}=\frac{\mu_0I}{4\pi(R^2+z^2)^{3/2}}\vec{dl}\wedge\vec{PM}\)
2 pts
\(\vec{PM}=-R\cos\theta\vec{e_x}-R\sin\theta\vec{e_y}+z\vec{e_z}\) et
\(\vec{dl}=-Rd\theta\sin\theta\vec{e_x}+Rd\theta\cos\theta\vec{e_y}\)
1 pt
\(d\vec B(M)=\frac{\mu_0I}{4\pi(R^2+z^2)^{3/2}}\left[\begin{array}{c}-Rd\theta\sin\theta \\ Rd\theta\cos\theta \\ 0 \end{array}\right. \wedge \left[\begin{array}{c} -R\cos\theta \\ -R\sin\theta \\ z \end{array}\right.= \frac{\mu_0I}{4\pi(R^2+z^2)^{3/2}} \left[\begin{array}{c} zR\cos\theta d\theta \\ zR\sin\theta d\theta \\R^2d\theta \end{array}\right.\)
2 pts