Champ au centre d'un solénoïde [Les courants stationnaires : champ et potentiel vecteur magnétostatiques]

Champ au centre d'un solénoïde

Durée : 12 mn

Note maximale : 5

Question

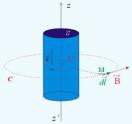
Un cylindre conducteur infiniment long, d'axe $z'z$ et de rayon $a$ est parcouru par un courant continu d'intensité $I$ , la densité de courant $\vec j=j\vec{e_z}$ y est uniforme.

En tenant compte de la leçon 1-1, donner la relation qui existe entre $I$ et $j$ .
Quelle est la direction du champ magnétostatique créé par le conducteur en un point $M$ ?
En appliquant le théorème d'Ampère, calculer le module du champ en fonction de la distance $r$ du point $M$ à l'axe $z'z$ .

Solution

1- $\vec j$ étant uniforme, on a :

$I=\int_s\int\vec j.\vec{dS}=\int_s\int j.dS=j\int_s\int dS=j.S=j\pi a^2$

2pts

2- Que le point $M$ soit à l'intérieur ou a l'extérieur du conducteur, le plan $Mz'z$ est un plan de symétrie auquel $\vec B(M)$ est donc perpendiculaire : le champ est orthoradial.

Comme pour le fil infiniment long, les lignes de de champ sont des cercles d'axe $z'z$ .

Le conducteur étant infiniment long, une translation ou une rotation par rapport à $z'z$ laisse le système invariant: $B(M)=B(r)$ et sur une ligne de champ comme $r = cte, B(M) = cte$ .

1pt

3- Le contour d'Ampère est donc un cercle de rayon $OM = r$ .

M extérieur au conducteur: $r >a$ :
$\oint_c\vec B.\vec{dl}=\oint_cB.dl=B\int_cdl=B.2\pi r=\mu_0I$ , d'où : $B(M)=\frac{\mu_0I}{2\pi r}$
M intérieur au conducteur : $r < a$ :
$\oint_c\vec B.\vec{dl}=B2\pi r=\mu_0\int_c\int\vec j.\vec{dS'}=js'=\frac{I}{\pi a^2}\pi r^2$ d'où $B(M')=\frac{\mu_0I}{2\pi}.\frac{r}{a^2}$

2pts