Champ créé par un tore cylindrique [Les courants stationnaires : champ et potentiel vecteur magnétostatiques]

Champ créé par un tore cylindrique

Durée : 10 mn

Note maximale : 5

Question

Sur un tore circulaire d'axe $z'z$ , de section droite carrée de coté $2a$ , on enroule $N$ spires régulièrement distribuées d'un fil conducteur parcouru par un courant d'intensité $I$ . Le tore a pour rayon moyen $R$ .

Déterminer le champ magnétostatique crée par ce tore en un point $M$ situé soit à l'extérieur, soit à l'intérieur du volume torique.

Solution

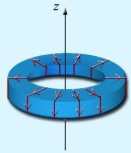
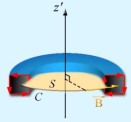
Que le point $M$ soit intérieur ou extérieur au volume torique, le plan $Mz'z$ est un plan de symétrie du système : $\vec B(M)$ est perpendiculaire à ce plan.

Une rotation du tore par rapport à $z'z$ laisse le système invariant et $B(M)=B(r,z)$

$\oint_c\vec B.\vec{dl}=\int_cB.dl=B.2\pi r$

Si $M$ est intérieur : $\mu_0\sum I=\mu_0NI$ et $B=\frac{\mu_0NI}{2\pi r}$ avec $R-a < r < R+a$
Si $M$ est extérieur : $\mu_0\sum I=0$ et $B=0$