Circuit RL
Partie
Question
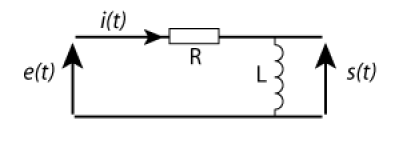
Montrer que le circuit ci-dessous est un circuit du premier ordre, dans lequel que les tensions d'entrée \(e(t)\) et l'intensité \(i(t)\) sont liées par une équation du type:
\(\displaystyle{\tau \frac{\mathrm di}{\mathrm dt} + i(t) = f(e(t))}\)
où \(\tau\) est la constante de temps du circuit.
Exprimer \(\tau\) en fonction des valeurs des composants du circuit.
Aide simple
L'intensité est la même dans \(\mathrm L\) et \(\mathrm R\)
Aux bornes de \(\mathrm L\) : \(\displaystyle{u(t) = \mathrm L\frac{\mathrm di}{\mathrm dt}}\)
Solution simple

\(\displaystyle{\tau=\frac{\mathrm L}{\mathrm R}}\)
Solution détaillée

La tension \(e(t)\) est la somme des tensions aux bornes des deux dipôles :
\(e(t) = u_\mathrm L + u_\mathrm R\)
Soit \(i(t)\) l'intensité du courant à travers les deux dipôles :
\(u_\mathrm R = \mathrm Ri(t)\)
\(\displaystyle{u_\mathrm L= \mathrm L\frac{\mathrm di}{\mathrm dt}}\)
d'où :
\(\displaystyle{e(t) = \mathrm Ri(t)+\mathrm L\frac{\mathrm di}{\mathrm dt}}\)
en divisant par \(\mathrm R\) , il vient :
\(\displaystyle{\begin{array}{lll}\frac{e(t)}{\mathrm R} &=& i(t)+\frac{\mathrm L}{\mathrm R}\frac{\mathrm di}{\mathrm dt}\\&=&i(t)+\tau\frac{\mathrm di}{\mathrm dt}\end{array}}\)
Le circuit est du premier ordre, et sa constante de temps est :
\(\displaystyle{\tau=\frac{\mathrm L}{\mathrm R}}\)