Réponse à une excitation harmonique
Partie
Question
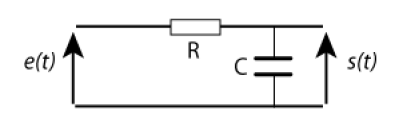
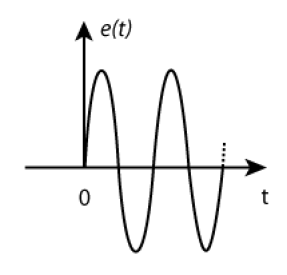
Soit le circuit ci-contre, dans lequel \(e(t)\) a l'allure ci-dessous
(\(t<0\) : \(e(t)=0\) ;\( t=0 \): \(e(t)=\mathrm E_\mathrm m\sin\omega t\))
Montrer que \(s(t)\) a pour équation:
\(s(t)=-\mathrm S_\mathrm m\sin\varphi.\mathrm e^{-t/\tau}+\mathrm S_\mathrm m\sin(\omega t+\varphi)\).
Donner les expressions de \(\mathrm S_\mathrm m\) et \(\varphi\) en fonction de et \(\mathrm E_\mathrm m\), \(\mathrm R\), \(\mathrm C\) et \(\omega\).
Aide simple
Chercher une solution particulière variant sinusoïdalement dans le temps
Aide détaillée
Utiliser l'écriture complexe des tensions sinusoïdales
Solution simple
\(\displaystyle{S_m=\frac{E_m}{\sqrt{1+(\mathrm{RC}\omega)^2}}}\)
\(\mathrm{tg }\varphi=-\mathrm{RC}\omega\)
Solution détaillée
La tension de sortie est \(s(t)\) solution de l'équation différentielle :
\(\displaystyle{\tau\frac{\mathrm ds}{\mathrm dt}+s(t)=e(t)}\) avec \(\tau=\mathrm{RC}\)
dont la solution est :
\(s(t)=\mathrm{Ae}^{-t/\tau}+\mathrm{SP}\)
où \(\mathrm{SP}\) est une solution particulière de l'équation complète.
Détail du calcul : voir circuit RC
Comme \(e(t)\) est de la forme
\(\displaystyle{e(t)=\mathrm E_m\sin\omega t=\mathrm E_m\cos\left(\omega t-\frac{\pi}{2}\right)}\)
on cherche une solution particulière de la forme :
\(\displaystyle{s(t)=\mathrm S_m\cos(\omega t+\phi)=\mathrm S_m\sin(\omega t+\varphi)}\)
\(\displaystyle{\left(\varphi=\phi-\frac\pi2\right)}\)
en utilisant la notation complexe
\(\begin{array}{lll}\underline e(t)&=&\mathrm E_m\mathrm e^{j\omega t}\mathrm e^{-j\pi/2}\\&=&-j\mathrm E_m\mathrm e^{j\omega t}\end{array}\)
\(\begin{array}{lll}\underline s(t)&=&\mathrm S_m\mathrm e^{j\omega t}\mathrm e^{j\phi}\\&=&-j\mathrm S_m\mathrm e^{j\omega t}\mathrm e^{j\varphi}\end{array}\)
d'où : \(\displaystyle{\frac{s(t)}{e(t)}=\frac{\mathrm S_m\mathrm e^{j\varphi}}{\mathrm E_m}}\)
or le rapport des tensions complexes est égal au rapport des impédances complexes correspondantes :
\(\displaystyle{\frac{s(t)}{e(t)}=\frac{\frac{1}{j\mathrm C\omega}}{\mathrm R+\frac{1}{j\mathrm C\omega}}=\frac1{1+j\mathrm R\mathrm C\omega}}\)
En identifiant les deux expressions :
\(\displaystyle{\frac{\mathrm S_m}{\mathrm E_m}\mathrm e^{j\varphi}=\frac1{1+j\mathrm R\mathrm C\omega}}\)
d'où :
\(\displaystyle{\mathrm S_m=\frac{\mathrm E_m}{\sqrt{1+(\mathrm R\mathrm C\omega)^2}}}\)
et : \(\mathrm{tg }\varphi=-\mathrm{RC}\omega\)
La solution générale de l'équation complète est donc :
\(s(t)=\mathrm{Ae}^{-t/\tau}+S_m\sin(\omega t+\varphi)\)
où \(S_m\) et \(\varphi\) ont les valeurs déterminées précédemment.
Jusqu'à \(t=0\), \(e(t)=0\) donc \(s(t)=0\). Comme la charge d'un condensateur varie de façon continue, pour \(t=0\):
\(s(0)=0=\mathrm A+S_m\sin\varphi\)
d'où :
\(\mathrm A=-S_m\sin\varphi\)
et finalement :
\(\displaystyle{s(t)=-\mathrm S_m\sin\varphi.\mathrm e^{-t/\tau}+\mathrm S_m\sin(\omega t+\varphi)}\)
courbe