Diviseur RC-RC
Partie
Question
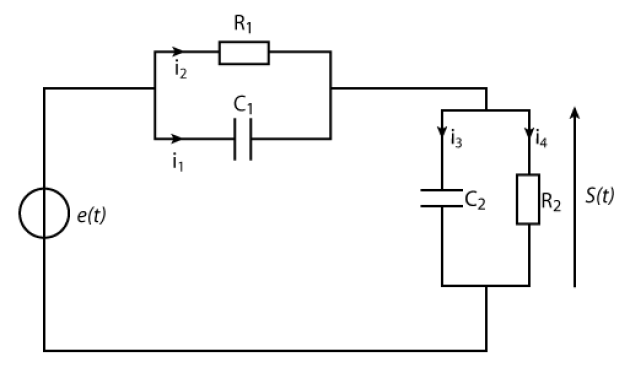
On applique à l'entrée du diviseur de tension \(e(t)\) \(\mathrm{RC}-\mathrm{RC}\) ci-dessous une tension \(e(t)\) de forme quelconque.
Etablir l'équation différentielle liant \(s(t)\) à \(e(t)\) et aux paramètres du circuit.
Aide simple
Chercher une solution particulière variant linéairement dans le temps
Aide détaillée
Lois des nœuds et des mailles
Solution simple
\(\displaystyle{\frac{\mathrm ds}{\mathrm dt}(\mathrm C_1+\mathrm C_2)+s\left(\frac{1}{\mathrm R_1}+\frac{1}{\mathrm R_2}\right)=\mathrm C_1\frac{\mathrm de}{\mathrm dt}+\frac e{\mathrm R_1}}\)
Solution détaillée
L'application de la loi aux nœuds donne :
\(i=i_1+i_2=i_3+i_4\) \((1)\)
L'application de la loi aux mailles donne :
\(e(t)=\mathrm Ri_2+s(t)\)
d'où :\(\displaystyle{i_2=\frac{e(t)-s(t)}{\mathrm R_1}}\)
La tension est la même aux bornes de \(\mathrm R_1\) et \(\mathrm C_1\):
\(\displaystyle{\mathrm R_1i_2=\frac{q_1}{\mathrm C_1}}\) où \(q_1\) est la charge de \(\mathrm C\) ???
d'où :
\(q_1=\mathrm R_1\mathrm C_1i_2\)
l'intensité \(i_1\) est liée aux variations de charge de \(\mathrm C_1\)
\(\displaystyle{i_1=\frac{\mathrm dq_1}{\mathrm dt}=\mathrm R_1\mathrm C_1\frac{\mathrm di_Z}{\mathrm dt}}\)
en remplaçant \(i_Z\) par son expression
\(\displaystyle{i_1=\mathrm C_1\left(\frac{\mathrm de}{\mathrm dt}-\frac{\mathrm ds}{\mathrm dt}\right)}\)
à la sortie :
\(\displaystyle{s(t)=\mathrm R_2i_4\Rightarrow i_4=\frac{s(t)}{\mathrm R_2}}\)
et comme :
\(\displaystyle{\mathrm R_2i_4=\frac{q_2}{\mathrm C_2}}\)
\(\displaystyle{i_3=\frac{\mathrm dq_{Z}}{\mathrm dt}=\mathrm R_2\mathrm C_2\frac{\mathrm di_4}{\mathrm dt}=\mathrm C\frac{\mathrm ds}{\mathrm dt}}\)
En remplaçant les intensités par leurs expressions en fonction de \(e(t)\) et \(s(t)\) dans l'équation \((1)\):
\(\displaystyle{\mathrm C_1\left(\frac{\mathrm de}{\mathrm dt}-\frac{\mathrm ds}{\mathrm dt}\right)+\frac{e(t)-s(t)}{\mathrm R_1}=\mathrm C_2\frac{\mathrm ds}{\mathrm dt}+\frac{s(t)}{\mathrm R_2}}\)
en séparant \(e\) et \(s\):
\(\displaystyle{(\mathrm C_1+\mathrm C_Z)\frac{\mathrm ds}{\mathrm dt}+\left(\frac{1}{\mathrm R_1}+\frac{1}{\mathrm R_2}\right)s(t)=\mathrm C_1\frac{\mathrm de}{\mathrm dt}+\frac{e(t)}{\mathrm R_1}}\)
Question
Les deux condensateurs étant déchargés, on applique au circuit une tension d'entrée définie par:
\(\mathrm e(t)=0\) pour \(t<0\) ;
\(\mathrm e(t)=\mathrm{a}.t\) pour \(t\ge0\) (\(\mathrm a>0\))
Etablir l'équation de \(s(t)\) et sa valeur asymptotique quand \(t\) tend vers l'infini.
Application numérique:
1. \(\mathrm R_1=\mathrm{9 M}\Omega\) ; \(\mathrm C_1=\mathrm{3 pF}\) ; \(\mathrm R_2=\mathrm{1 M}\Omega\) ; \(\mathrm C_2=\mathrm{20 pF}\)
2. \(\mathrm R_1=\mathrm{9 M}\Omega\) ; \(\mathrm C_1=\mathrm{1 pF}\) ; \(\mathrm R_2=\mathrm{1 M}\Omega\) ; \(\mathrm C_2=\mathrm{20 pF}\)
3. \(\mathrm R_1=\mathrm{9 M}\Omega\) ; \(\displaystyle{\mathrm C_1=\frac{20}{9}\mathrm{ pF}}\) ; \(\mathrm R_2=\mathrm{1 M}\Omega\) ; \(\mathrm C_2=\mathrm{20 pF}\)
Aide simple
Chercher une solution particulière variant linéairement dans le temps
Aide détaillée
Lois des nœuds et des mailles
Solution simple
\(\displaystyle{s(t)=\mathrm a\left(\tau-\frac{\mathrm R_1.\mathrm R_2}{\mathrm R_1+\mathrm R_2}\mathrm C_1\right)\mathrm e^{{-t}/{\tau}}+\mathrm a\frac{\mathrm R_2}{\mathrm R_1+\mathrm R_2}(t+\mathrm R_1\mathrm C_1-\tau)}\)
1. \((R_1C_1-\tau)>0\)
2. \((R_1C_1-\tau)<0\)
3. \((R_1C_1-\tau)=0\)
Solution détaillée
Si on pose \(\mathrm C=\mathrm C_1+\mathrm C_2\), \(\displaystyle{\frac1{\mathrm R}=\frac1{\mathrm R_1}+\frac1{\mathrm R_2}}\)
Il vient
\(\displaystyle{\tau\frac{\mathrm ds}{\mathrm dt}+s(t)=\mathrm R\mathrm C_1\frac{\mathrm de}{\mathrm dt}+\frac{\mathrm R}{\mathrm R_1}e(t)}\)
avec \(\tau=\mathrm{RC}\)
Comme \(e(t)=\mathrm at\), alors \(\displaystyle{\frac{\mathrm de}{\mathrm dt}=\mathrm a}\)
Et l'équation différentielle donnant \(s(t)\) est :
\(\displaystyle{\tau\frac{\mathrm ds}{\mathrm dt}+s(t)=\mathrm R\mathrm C_1\mathrm a+\frac{\mathrm{Ra}t}{\mathrm R_1}}\)
dont la solution est
\(s(t)=\mathrm{Ae}^{-t/\tau}+\mathrm{SP}\)
où \(\mathrm{S.P}\) est une solution particulière de l'équation complète ; comme le second membre est un polynôme du premier degré en \(t\), on cherche une solution sous la forme :
\(s(t)=\mathrm bt+\mathrm c\), donc \(\displaystyle{\frac{\mathrm ds}{\mathrm dt}=\mathrm b}\),
ce qui donne
\(\displaystyle{\mathrm b\tau+\mathrm bt+\mathrm c=\mathrm R\mathrm C_1\mathrm a+\frac{\mathrm R}{\mathrm R_1}\mathrm at}\)
en identifiant terme à terme :
\(\displaystyle{\mathrm b=\mathrm a\frac{\mathrm R}{\mathrm R_1}}\)
\(\mathrm b\tau+\mathrm c=\mathrm R\mathrm C_1\mathrm a\Leftrightarrow \mathrm a\tau+\mathrm c=\mathrm R\mathrm C_1\mathrm a\)
\(\mathrm c=\mathrm a(\mathrm R\mathrm C_1-\tau)\)
d'où la solution particulière
\(\displaystyle{s(t)=\mathrm a\frac{\mathrm R}{\mathrm R_1}t+\mathrm a(\mathrm R\mathrm C_1-\tau)}\)
et la solution générale
\(\displaystyle{s(t)=\mathrm{Ae}^{-t/\tau}+\mathrm a\frac{\mathrm R}{\mathrm R_1}(t-\tau)+\mathrm a(\mathrm R\mathrm C_1-\tau)}\)
comme jusqu'à \(t=0\), \(e=0\), on a aussi ; et puisque la charge d'un condensateur varie de façon continue :
\(s(0)=0=\mathrm A+\mathrm a(\mathrm R\mathrm C_1-\tau)\)
d'où \(\mathrm A=\mathrm a(\tau-\mathrm R\mathrm C_1)\)
finalement, en fonction de \(\mathrm R_1\), \(\mathrm R_2\), \(\mathrm C_1\), \(\mathrm C_2\):
\(\displaystyle{s(t)=\mathrm a\left(\tau-\frac{\mathrm R_1\mathrm R_2}{\mathrm R_1+\mathrm R_2}\mathrm C_1\right)\mathrm e^{-t/\tau}+\mathrm a\frac{\mathrm R_2}{\mathrm R_1+\mathrm R_2}(t+\mathrm R_1\mathrm C_1-\tau)}\)
Le premier terme tend vers zéro quand \(t\) tend vers l'infini, le second est une droite de pente \(\displaystyle{\mathrm a\frac{\mathrm R_2}{\mathrm R_1+\mathrm R_2}}\), qui coupe l'axe des \(t\) pour \(t=\tau-\mathrm R_1\mathrm C_1\)
Application numérique : \(\displaystyle{\mathrm a\frac{\mathrm R_2}{\mathrm R_1+\mathrm R_2}=\frac{\mathrm a}{10}}\);
1. \(\tau-R_1C_1=-\mathrm{6,3 }\mu\mathrm s\)
2. \(\tau-R_1C_1=-\mathrm{9,9 }\mu\mathrm s\)
3. \(\tau-R_1C_1=0\)
Question
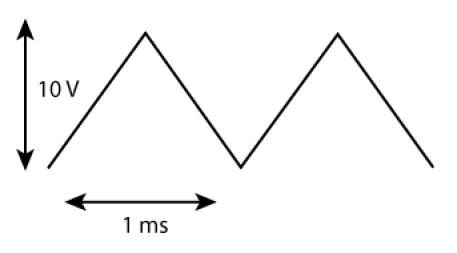
Le signal d'entrée est maintenant le "triangle" ci-dessous. Quelle est la réponse \(s(t)\) du circuit quand il est réalisé avec les valeurs numériques du 3. ?
Aide simple
Chercher une solution particulière variant linéairement dans le temps
Aide détaillée
Lois des nœuds et des mailles
