Charge d'un condensateur [Circuits du premier ordre]

Charge d'un condensateur

Partie

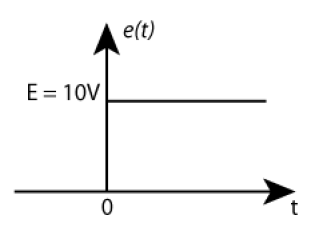
On applique à l'entrée du circuit ci-dessus l'échelon de tension dont on a représenté la courbe \(e(t)\) ci-dessous.

Question

Donner l'équation de \(s(t)\).

Aide simple

L'intensité est la même dans et \(\mathrm R\) et \(\mathrm C\).

Aide détaillée

L'intensité est due à la variation de charge du condensateur : \(i(t)=\mathrm dq/\mathrm dt\).

Solution simple

\(\displaystyle{s(t)=\mathrm E\left(1-\mathrm e^{-\frac{t}{\tau}}\right)}\)

Solution détaillée

1) Pour ce circuit, les tensions d'entrée et sortie sont liées par l'équation différentielle :

\(\displaystyle{e(t)=\tau\frac{\mathrm ds}{\mathrm dt}+s(t)}\) où \(\tau=\mathrm{RC}\)

( détail du calcul : cf circuit \(\mathrm{RC}\))

L'équation sans second membre s'écrit :

\(\displaystyle{\tau\frac{\mathrm ds}{\mathrm dt}+s(t)=0}\)

Elle a pour solution :

\(s(t)=\mathrm{Ae}^{-t/\tau}\)

La solution complète s'obtient en ajoutant une solution particulière de l'équation avec second membre.

Comme pour \(t>0\), \(e(t)=\mathrm E=cste\), on cherche une solution constante.

\(\displaystyle{\frac{\mathrm ds}{\mathrm dt}}\) s'annule donc, et la solution particulière est \(s(t)=\mathrm E\), d'où la solution générale \(s(t)=\mathrm{Ae}^{-t/\tau}+\mathrm E\)

pour \(t\le0\), comme \(e(t)=0\), \(s(t)=0\)

\(0=\mathrm A+\mathrm E \Leftrightarrow \mathrm A=-\mathrm E\)

finalement : \(\displaystyle{s(t)=\mathrm E\left(1-\mathrm e^{-\frac{t}{\tau}}\right)}\)

Question

Sachant que \(\mathrm R=10\mathrm{ k}\Omega\), \(\mathrm C=\mathrm{1 }\mu\mathrm F\), quelle est la valeur de \(s(t)\) pour \(\mathrm t=\mathrm{10 ms}\)?

Au bout de combien de temps aura-t-on :

\(\mathrm{s(t)=9,00 V}\) ?

\(\mathrm{s(t)=9,50 V}\) ?

\(\mathrm{s(t)=9,90 V}\) ?

Aide simple

L'intensité est la même dans et \(\mathrm R\) et \(\mathrm C\).

Aide détaillée

L'intensité est due à la variation de charge du condensateur : \(i(t)=\mathrm dq/\mathrm dt\).

Solution simple

\(\mathrm{6,3 V}\) ; \(\mathrm{23 ms} \); \(\mathrm{30 ms} \); \(\mathrm{46 ms}\)

Solution détaillée

\(\tau=\mathrm{RC}=10^4.10^{-6}=10^{-2}\mathrm{s}=\mathrm{10 ms}\)

pour \(t=\mathrm{10 ms}=\tau\)

\(\displaystyle{s(t)=10\left(1-\mathrm e^{-1}\right)=\mathrm{6,3 V}}\)

pour \(t\) quelconque (\(t\) en \(s\))

\(\displaystyle{s(t)=10\left(1-\mathrm e^{-100t}\right)}\)

donc,

si \(s(t)=\mathrm{9 V}\), \(\mathrm e^{-100t}=\mathrm{0,1}\), \(t=\mathrm{23 ms}\)

si \(s(t)=\mathrm{9,5 V}\), \(\mathrm e^{-100t}=\mathrm{0,05}\), \(t=\mathrm{30 ms}\)

si \(s(t)=\mathrm{9,9 V}\), \(\mathrm e^{-100t}=\mathrm{0,01}\), \(t=\mathrm{46 ms}\)

Question

On applique maintenant à l'entrée un signal \(e(t)\) en forme de créneau. Quelle doit être la période \(T\) du créneau pour que l'on puisse considérer que l'amplitude de \(s(t)\) est à \(\mathrm{1 \%}\) la même que celle de \(e(t)\)?