Application dérivée
Dans tout le paragraphe on notera \(\mathcal I\) un intervalle de \(\mathbf R\) non vide ni réduit à un point.
Définition :
Soit\( f\) une application de\( \mathcal I\) dans \(\mathbf R\), on dit que \(f\) est dérivable sur \(\mathcal I\) si \(f\) est dérivable en tout point de \(\mathcal I\). On note alors :
\(\displaystyle{f' :\mathcal I\rightarrow\mathbf R\quad x\mapsto f'(x)}\)
\(f'\) est l'application dérivée de \(f\) ou plus simplement la dérivée de \(f\).
Au lieu de \(f'\) on utilise également la notation différentielle :
\(\displaystyle{\frac{\textrm df}{\textrm dx} :\mathcal I\rightarrow\mathbf R\quad x\mapsto\frac{\textrm df}{\textrm dx}(x)}\) ou \(\displaystyle{\frac{\textrm d}{\textrm dx}f(x)}\)
Définition :
Si la fonction \(f'\) est continue sur \(\mathcal I\) on dit que \(f\) est continûment dérivable sur \(\mathcal I\) ou de classe \(\mathcal C^1\)sur \(\mathcal I\). On note \(\mathcal C^1(\mathcal I,\mathbf R)\) l'ensemble des fonctions de classe \(\mathcal C^1\) sur \(\mathcal I\).
Compte-tenu de ce qui a été vu à propos des fonctions dérivables en un point, on déduit immédiatement de la définition précédente que les polynômes, les fonctions sinus, cosinus et l'exponentielle sont de classe \(\mathcal C^1\) sur \(\mathbf R\), ainsi que les fonctions rationnelles sur tout intervalle qui ne contient pas de pôle (zéro du dénominateur), les fonctions logarithme et racine carrée sur \(]0,+\infty[\), la fonction tangente sur \(\displaystyle{]\frac{\pi}{2}+k\pi,\frac{\pi}{2}+(k+1)\pi[\quad(k\in\mathbf Z)}\).
Exemple : Exemple 1
Soit la fonction définie sur \(\mathbf R\) par :
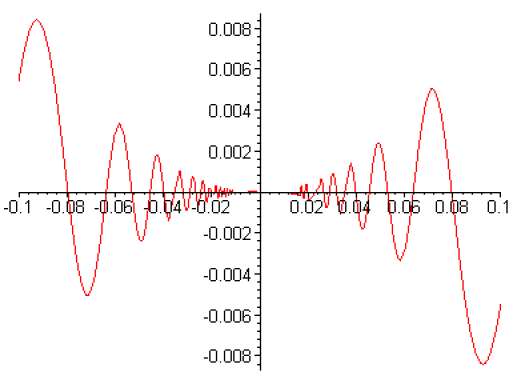
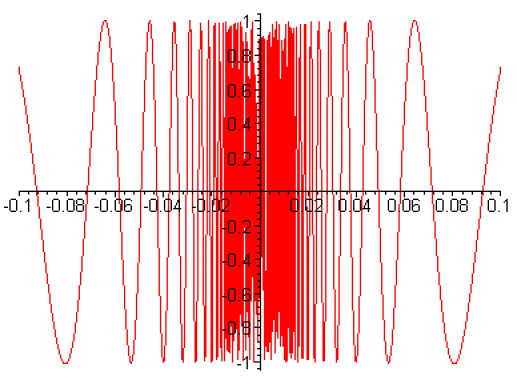
\(\displaystyle{\forall x\neq0\quad f(x)=x^2\sin\frac{1}{x}}\) et \(f(0)=0\)
On a \(\displaystyle{\forall x\neq0\frac{f(x)}{x}=x\sin\frac{1}{x}}\), d'où \(f\) est dérivable en \(0\) et \(f'(0) = 0\).
Mais pour tout \(x\) non nul, \(f\) est dérivable et \(\displaystyle{f'(x)=2x\sin\frac{1}{x}-\cos\frac{1}{x}}\). Le premier terme tend vers \(0\) et le second n'a pas de limite quand \(x\) tend vers \(0\). La fonction \(f'\) n'est pas continue en \(0\). La fonction est dérivable sur \(\mathbf R\) mais elle n'est pas de classe \(\mathcal C^1\) sur \(\mathbf R\).
Exemple : Exemple 2
Soit \(g\) la fonction définie sur \(\mathbf R\) par :
\(\displaystyle{\forall x\neq 0,~g(x)=\textrm e^{-\tfrac{1}{x^2}}}\) et \(g(0)=0\);
La fonction \(g\) est continue en \(0\) car \(\displaystyle{\lim_{x\to0}\textrm e^{-\tfrac{1}{x^2}}=0}\).
(on pose \(\displaystyle{h = \frac{1}{x}}\), on est alors ramené à étudier la fonction \(\displaystyle{h\mapsto\textrm e^{-h^2}}\) quand \(h\) tend vers \(+\infty\) et \(-\infty\), on fera de même pour les autres limites).
Pour tout \(x\) non nul la fonction \(g\) est dérivable et \(g'(x)=\frac{2}{x^3}e^{-\frac{1}{x^2}}\) ; la fonction \(g'\) est donc continue en tout point de \(\mathbf R^*\).
D'autre part : \(\displaystyle{\forall x\neq 0,~\frac{g(x)}{x}=\frac{\textrm e^{-\tfrac{1}{x^2}}}{x}}\) d'où \(\displaystyle{\lim_{x\to 0} \frac{g(x)}{x}=0}\). La fonction \(g\) est donc dérivable à l'origine et \(g'(0)=0\).
La fonction \(g'\), dérivée de \(g\), est continue en \(0\) car \(\displaystyle{\lim_{x\to 0}\frac{2}{x^3}\textrm e^{-\tfrac{1}{x^2}}=0}\). La fonction \(g\) est donc de classe \(\mathcal C^1\) sur \(\mathbf R\).
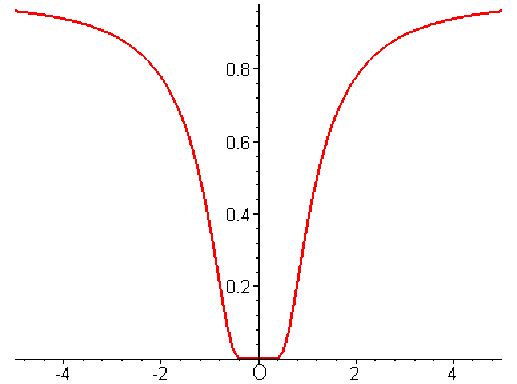
Remarque :
Il ne faut pas s'étonner du segment de droite autour du point \(\mathcal O\) de coordonnées \((0,0)\), le graphe est "très" aplati (plus que pour toute fonction polynomiale) en \(\mathcal O\).