Formule et inégalité de Taylor-Lagrange
Introduction
Dans tout ce paragraphe, on considérera, comme précédemment, un intervalle fermé, borné \([a,b],(a < b)\). Formule et inégalité de Taylor-Lagrange sont des généralisations du théorème et de l'inégalité des accroissements finis : l'expression ou la majoration en valeur absolue de \(f(b)-f(a)\) fait intervenir alors les dérivées successives (jusqu'à un ordre \(n\)) de \(f\) au point \(a\) ainsi que la dérivée d'ordre \(n+1\) de f en un point de l'intervalle \(]a, b[\).
Théorème de Taylor-Lagrange
Théorème :
Soit \(f\) une application de l'intervalle \([a,b]\) dans \(\mathbf R\) vérifiant les conditions suivantes :
pour tout \(k=0,1\cdots n, f^{(k)}\) existe et est continue sur \([a,b]\),
\(f^{(n+1)}\) existe sur \(]a,b[\).
Alors il existe \(c\in]a,b[\) tel que :
\(\displaystyle{f(b)-f(a)=(b-a)f'(a)+\frac{(b-a)^2}{2 !}f"(a)+\cdots+\frac{(b-a)^n}{n !}f^{(n)}(a)+\frac{(b-a)^{n+1}}{(n+1)!}f^{(n+1)}(c)}\)
Preuve :
On a signalé et on le remarque sur la formule proposée : pour \(n = 0\), il s’agit de la formule des accroissements finis. Comme dans le cas de la formule des accroissements finis la démonstration consiste à appliquer le théorème de Rolle à une certaine fonction. En effet, soit \(A\) le réel défini par l’égalité : \(\frac{(b-a)^{n+1}}{(n+1)!}A=f(b)-f(a)-\displaystyle{\sum_{k=1}^{n}}\frac{(b-a)^k}{k!}f^{(k)}(a)\).
Il s’agit de montrer que \(A=f^{(n+1)}(c)\) avec \(c\in]a,b[\).
On introduit, pour cela la fonction \(\phi\) définie par : \(\phi(x)=f(b)-f(x)-\displaystyle{\sum_{k=1}^n}\frac{(b-x)^k}{k!}f^{(k)}(x)-\frac{(b-x)^{n+1}}{(n+1)!}A\)
La fonction \(\phi\) vérifie toutes les conditions du théorème de Rolle. Il existe donc \(c\in]a,b[\) tel que \(\phi'(c)=0\). Or, on a :
\(\phi'(x)=-f'(x)-\displaystyle{\sum_{k=1}^n}\left(-\frac{(b-x)^{k-1}}{(k-1)!}f^{(k)}(x)+\frac{(b-x)^k}{k!}f^{(k+1)}(x)\right)+\frac{(b-x)^n}{n!}A\) ou encore :
\(\phi'(x)=-f'(x)+\displaystyle{\sum_{k=0}^{n-1}}\frac{(b-x)^{k}}{k!}f^{(k+1)}(x)-\displaystyle{\sum_{k=1}^{n}}\frac{(b-x)^{k}}{k!}f^{(k+1)}(x)+\frac{(b-x)^n}{n!}A\), d’où
\(\phi'(x)=\frac{(b-x)^n}{n!}(-f^{(n+1)}(x)+A)\).
Il existe donc \(c\in]a,b[\) tel que \(A=f^{(n+1)}(c)\).
On énonce encore le théorème de Taylor-Lagrange sous la forme suivante (\(\mathcal I\) n'est pas nécessairement fermé, borné).
Théorème :
Soit \(f\) une fonction \(n+1\) fois dérivable sur un intervalle \(\mathcal I\) et\( x_0\) un point de \(\mathcal I\) ;
alors, pour tout \(h\) réel tel que \(x_0+h\in\mathcal I\), il existe \(\theta_h\in]0,1[\) tel que :
\(\displaystyle{f(x_0+h)=f(x_0)+hf'(x_0)+\frac{h^2}{2!}f"(x_0)+\cdots+\frac{h^n}{n!}f^{(n)}(x_0)+\frac{h^{n+1}}{(n+1)!}f^{(n+1)}(x_0+\theta_hh)}\)
Preuve :
Dans le cas \(h> 0\) on applique le théorème précédent avec \(x_0=a,x_0+h=b\), sinon on reprend la démonstration.
Inégalité de Taylor-Lagrange
Théorème :
Soit \(f\) une fonction \(n+1\) fois dérivable sur un intervalle\( \mathcal I\) ; on suppose qu'il existe \(\mathcal M\) tel que \(\forall x \in \mathcal I, ~\displaystyle{\vert f^{(n+1)}(x)\vert\leq\mathcal M}\). Alors on a :
\(\displaystyle{\forall x_1\in\mathcal I,\forall x_2\in\mathcal I}\)
\(\displaystyle{\left\vert f(x_2)-f(x_1)-\sum_{k=1}^{n}\frac{(x_2-x_1)^k}{k!}f^{(k)}(x_1)\right\vert\leq\mathcal M\frac{\vert x_2-x_1\vert^{n+1}}{(n+1)!}}\)
Preuve :
On déduit de la formule de Taylor-Lagrange l'inégalité de Taylor-Lagrange; comme dans le cas du théorème des acroissements finis et pour des raisons analogues, elle est plus générale que la formule.
Applications
Calcul d'erreurs
Considérons la fonction sinus sur l'intervalle\( \displaystyle{\left[0,\frac{\pi}{6}\right]}\), l'inégalité de Taylor-Lagrange s'écrit
pour \(n=2\) et \(\displaystyle{\forall x\in\left[0,\frac{\pi}{6}\right],\vert\sin x-x\vert<\frac{x^3}{6}}\)
pour \(n=4\) et \(\displaystyle{\forall x\in\left[0,\frac{\pi}{6}\right],\left\vert\sin x-x-\frac{x^3}{6}\right\vert<\frac{x^5}{120}}\).
Ainsi, en remarquant que la valeur \(\displaystyle{\frac{\pi}{6}}\) n'est pas "petite", on note que, sur l'intervalle \(\displaystyle{\left[0,\frac{\pi}{6}\right]}\), en remplaçant \(\sin x\) par \(x\) on commet une erreur majorée par \(\displaystyle{\frac{x^3}{6}}\), soit de l'ordre de \(2.10^{-2}\).
En remplaçant\( \sin x\) par\( \displaystyle{x-\frac{x^3}{6}}\) on commet une erreur majorée par \(\displaystyle{\frac{x^5}{120}}\) soit de l'ordre de \(3.10^{-4}\) .
Plus \(n\) est grand, meilleure est l'approximation.
L'animation montre les approximations successives de la fonction sinus par ses premiers développements de Taylor.
Somme de série
On se propose de montrer l'égalité :
\(\displaystyle{\textrm e^x=\lim_{n\to+\infty}\left(1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}\right)}\).
La fonction exponentielle étant de classe \(\mathcal C^{\infty}\) on a donc pour tout entier \(n\) :
\(\displaystyle{\forall x\in\mathbf R,~\textrm e^x=1+x+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}+\frac{x^{n+1}}{(n+1)!}}\textrm e^{\theta x},(0<\theta<1)\)
On en déduit :
\(\displaystyle{\forall x\in\mathbf R, \left\vert\textrm e^x-\sum_{k=0}^{n}\frac{x^k}{k!}\right\vert\leq\frac{\left\vert x^{n+1}\right\vert}{(n+1)!}\textrm e^{\vert x\vert}}\)
or , \(\displaystyle{\lim_{n\to+\infty}\frac{\vert x^{n+1}\vert}{(n+1)!}=0}\), d'où l'égalité recherchée.
Il s'agit là d'une série : on considère une suite \((u_n)\) définie, pour \(x\) fixé, par \(\displaystyle{u_n=\frac{x^n}{n!}}\), à laquelle on associe une autre suite \((s_n)\) définie par \(\displaystyle{s_n=\sum_{k=0}^{n}u_k}\)et on étudie la suite \((s_n)\) .
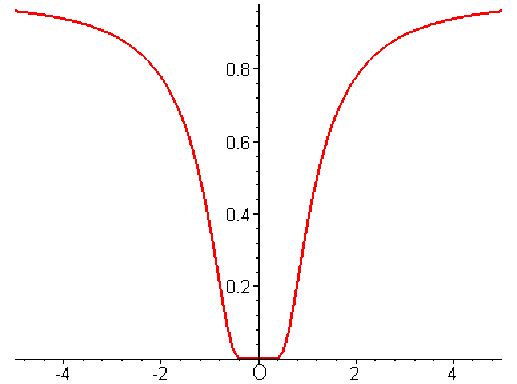
Étude de la dérivabilité d'une fonction en 0
\(\displaystyle{\forall x\neq0\quad g(x)=\textrm e^{-\tfrac{1}{x^2}}}\) et \(g(0)=0\)
Nous avons vu que \(g\) est continue et dérivable en \(0\), nous allons montrer qu'elle est indéfiniment dérivable en \(0\) et que toutes ses dérivées en \(0\) sont nulles. On a
\(\displaystyle{\forall x\neq0\quad g'(x)=-\frac{2}{x^3}\textrm e^{-\tfrac{1}{x^2}}}\)
on peut donc conjecturer que :
\(\displaystyle{\forall x\neq0,\forall n\geq 1\quad g^{(n)}(x)=\mathcal P\left(\frac{1}{x}\right)\textrm e^{-\tfrac{1}{x^2}}}\)
où \(\mathcal P\) est un polynôme à coefficients réels, en effet supposons que la dérivée \(n\)-ième est de cette forme on a :
\(\displaystyle{g^{(n+1)}(x)=\left(-\frac{1}{x^2}\mathcal P'\left(\frac{1}{x}\right)+\frac{2}{x^3}\mathcal P\left(\frac{1}{x}\right)\right)\textrm e^{-\tfrac{1}{x^2}}=\mathcal Q\left(\frac{1}{x}\right)\textrm e^{-\tfrac{1}{x^2}}}\)
où \(\mathcal Q\) est un polynôme à coefficients réels. On montre alors, en posant \(h = 1/x\),
\(\displaystyle{\lim_{x\to0}\mathcal Q\left(\frac{1}{x}\right)\textrm e^{-\tfrac{1}{x^2}}=0}\)
La fonction \(g\) est indéfiniment dérivable en \(0\) et toutes ses dérivées en \(0\) sont nulles. On a donc, par le théorème de Taylor-Lagrange :
\(\displaystyle{\forall x\neq0,\forall n\geq 1,~g(x)=\frac{x^{n+1}}{(n+1)!}g^{(n+1)}(\theta_x)}\)