Cas d'une symétrie axiale
Une distribution de charges sources a une symétrie axiale si la densité de charges en un point \(M\) est uniquement fonction de la distance \(r\) à un axe \(\Delta\).
Exemples :
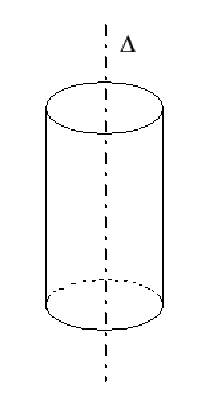
cylindre métallique chargé en surface
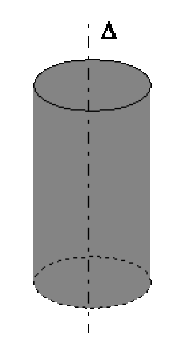
nuage de charges cylindrique de densité volumique \(\rho = \mathrm{cte}\)
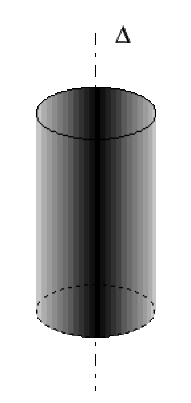
nuage de charges cylindrique de densité volumique \(\rho = f(r)\)
Par symétrie, le champ est radial (loin des bords de la source)
La surface de Gauss la plus adaptée est un cylindre axé sur \(\Delta\) et passant par le point d'étude \(M\) (celui-ci peut être intérieur ou extérieur à la source)
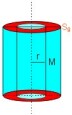
point d'étude extérieur à la source
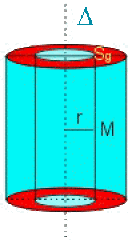
point d'étude intérieur à la source
3.
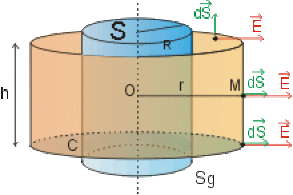
Sur les sections droites \(S\) du cylindre \(S_g\), les vecteurs \(\vec E\) et \(\mathrm d \vec S\) sont orthogonaux, le flux de \(\vec E\) à travers \(S\) est donc nul. Le flux de \(\vec E\) à travers la surface de Gauss fermée est réduit au flux à travers la surface latérale.
\(\Phi = \iint_{S_g} \vec E . \mathrm d \vec S = \iint_{S_{\textrm{lat\'erale}}} \vec E . \mathrm d \vec S + \iint_S \vec E . \mathrm d \vec S = \iint_{S_{\textrm{lat\'erale}}} \vec E . \mathrm d \vec S\)
Sur la surface latérale \(\vec E\) et \(\mathrm d \vec S\) sont colinéaires donc le flux se réduit à :
\(\Phi = \iint_{S_{\textrm{lat\'erale}}} \vec E . \mathrm d \vec S = \iint_{S_{\textrm{lat\'erale}}} E . \mathrm d S\)
\(E\) est le même en tout point de \(S_g\) et peut donc être sorti de l'intégrale :
\(\Phi = \iint_{S_{\textrm{lat\'erale}}} E . \mathrm d S = E~\iint_{S_{\textrm{lat\'erale}}} \mathrm d S = E ~ S_{\textrm{lat\'erale}}\)
or la surface latérale de la surface de Gauss est égale à \(2 \pi r h\)
\(\Phi = E . 2 \pi r h\)
Il ne reste plus qu'à évaluer la charge \(Q_i\) intérieure au volume délimité par \(S_g\) suivant la distribution considérée. La théorème de Gauss permet alors de déterminer le champ \(E\) en écrivant :
\(\Phi = E . 2 \pi r h = \frac{Q_i}{\epsilon_0}\)