Stigmatisme rigoureux
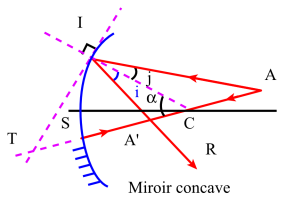
L'équation \(\frac{1}{\overline{\mathrm{CA}}}+\frac{1}{\overline{\mathrm{CA'}}}=\frac{2~\cos~\alpha}{\mathrm r}\) permet de calculer \(\overline{\mathrm{CA'}}\),
soit : \(\overline{\mathrm{CA'}}=\mathrm r~\frac{\overline{\mathrm{CA}}}{2~\overline{\mathrm{CA}}~\cos~\alpha~-~\mathrm r}\)
Le second membre de cette expression n'est généralement pas constant pour un point \(\mathrm A\) donné, car il est fonction de l'angle \(\alpha\). Autrement dit, \(\mathrm{A'}\) ne peut être considéré comme l'image[1] de la source ponctuelle \(\mathrm A\) puisque sa position dépend du choix du rayon incident \(\mathrm{AI}\).
Attention :
Un miroir sphérique n'est donc pas rigoureusement stigmatique pour un point quelconque de l'espace.
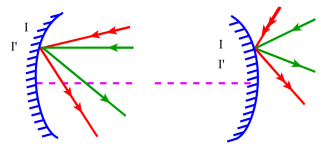
En fait, pour qu'il y ait stigmatisme[2] absolu il faut que dans l'expression donnant \(\overline{\mathrm{CA'}}\), le terme en \(\cos~\alpha\) soit nul ou constant. La première condition exige que \(\overline{\mathrm{CA}}=0\) ; la seconde, quant à elle, nécessite que les points d'incidence de tous les rayons lumineux soient confondus. Physiquement cela signifie que :
Attention :
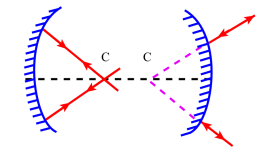
Les seuls points rigoureusement stigmatiques pour un miroir sphérique sont :
son centre de courbure C
les points de sa surface réfléchissante.
Observer
Le stigmatisme rigoureux du centre du miroir sphérique concave est illustré par la vidéo suivante :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.