Ce qu'il faut retenir :
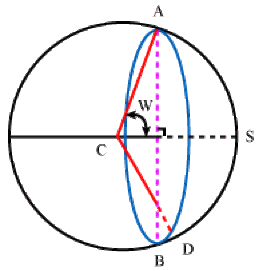
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
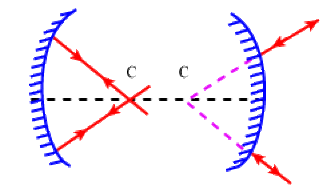
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
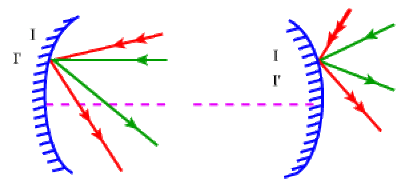
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
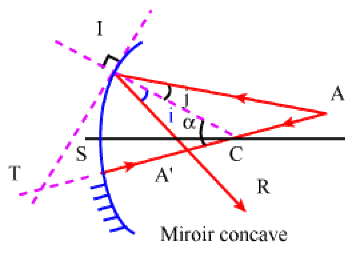
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
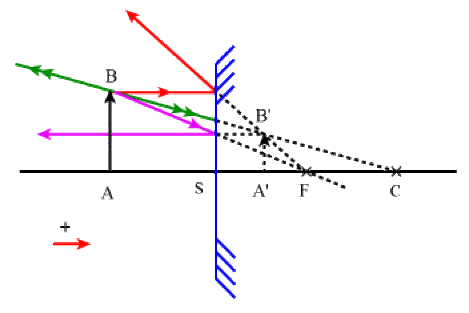
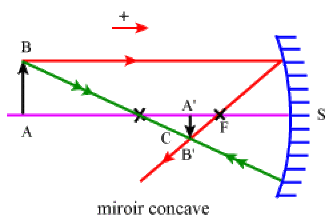
\(p= \overline{SA} \quad p'=\overline{SA'} \quad f=\overline{SF}\)
\(\frac{1}{p'} + \frac{1}{p} = \frac{1}{f} \quad \textrm{ avec }\quad \gamma = \frac{\overline{A'B'}}{\overline{AB}} = - \frac{p'}{p}\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

\(\sigma= \overline{FA} \quad \sigma'=\overline{FA'} \quad\)
\(\textrm{ et }\quad f=\overline{SF} = \overline{SF'} =f' \qquad \textrm{(attention !)}\)
\(\sigma \sigma' = f^{2} \quad \textrm{ avec }\quad \gamma = \frac{\overline{A'B'}}{\overline{AB}} = - \frac{\sigma'}{f} = - \frac{f}{\sigma}\)
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.