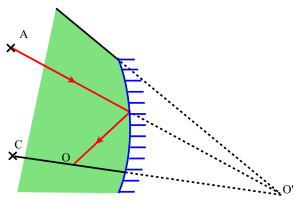
Champ d'un miroir sphérique
La définition du champ donnée pour un miroir plan demeure valable pour les miroirs sphériques.
Un point \(\mathrm A\) de l'espace est vu par réflexion par l'oeil placé en \(\mathrm O\) si, parmi tous les rayons issus de \(\mathrm A\), il en est un qui parvient à \(\mathrm O\) : ce rayon joint \(\mathrm A\) à l'image \(\mathrm{O'}\) de \(\mathrm O\), il se réfléchit en \(\mathrm I\) vers \(\mathrm O\).Le champ du miroir est délimité par le cône de sommet \(\mathrm{O'}\) s'appuyant sur son contour.
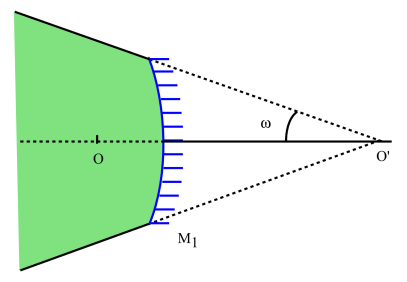
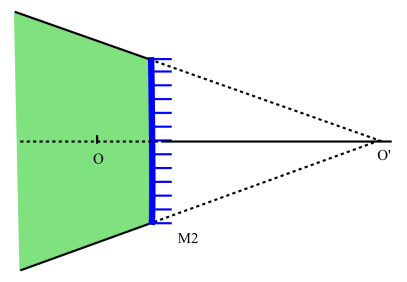
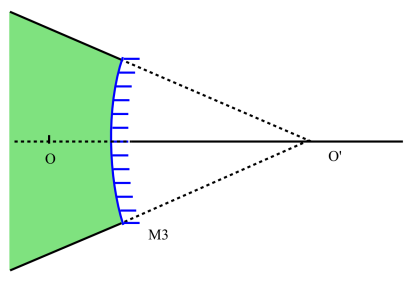
La figure ci-dessus représente trois miroirs de mêmes dimensions :
M1 est concave
M2 est plan et
M3 est convexe
Les distances focales de M1 et M3 sont égales, \(\mathrm O\) occupe la même position devant les trois miroirs.
On a construit l'image \(\mathrm{O'}\) dans les trois cas ; on constate que les demi-angles de champ croissent de M1 vers M3.
Ce qui justifie l'emploi de miroirs convexes comme rétroviseur (les distances ne sont alors pas conservées, c'est pourquoi on associe un miroir plan et un miroir convexe).
Observer
Le champ du miroir sphérique est illustré par les vidéos suivantes :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.