Stigmatisme approché. Conditions de Gauss [Miroir Sphérique]

Stigmatisme approché. Conditions de Gauss

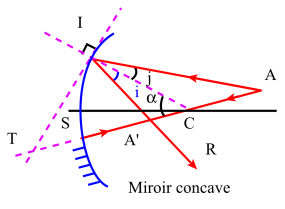
On sait qu'il y a stigmatisme^[1] approché chaque fois qu'il est possible d'obtenir d'un objet^[2] ponctuel A une image^[3] A' quasi ponctuelle. Dans le cas présent, cela revient à dire, que dans l'expression donnant \(\overline{\mathrm{CA'}}\): \(\overline{\mathrm{CA'}}=\mathrm r~\frac{\overline{\mathrm{CA}}}{2~\overline{\mathrm{CA}}~\cos~\alpha~-~\mathrm r}\) le terme en \(\cos~\alpha\) doit :

soit être négligeable,
soit conserver une valeur à peu près constante pour l'ensemble des rayons lumineux émis par le point source \(\mathrm A\).

La première condition est réalisée si \(\mathrm A\) est au voisinage immédiat du centre \(\mathrm C\) du miroir. En effet on peut écrire, en posant \(\overline{\mathrm{CA}}=\varepsilon~\) :

\(\overline{\mathrm{CA'}}=\mathrm r~\frac{\varepsilon}{2~\varepsilon~\cos~\alpha~-~\mathrm r}=\frac{-~\varepsilon}{1~-~2~\frac{\varepsilon}{\mathrm r}~\cos~\alpha}=-\varepsilon~\big(1~+~2~\frac{\varepsilon}{\mathrm r}~\cos~\alpha\big)\)

soit, puisque \(\varepsilon\ll r\) : \(\overline{\mathrm{CA'}}=-\varepsilon=\overline{\mathrm{AC}}\)

Cette expression qui ne dépend plus de l'angle \(\alpha\) nous montre donc que :

Attention :

Le stigmatisme approché est vérifié, quelle que soit l'ouverture du faisceau^[4] de lumière incidente, pour tous les points situés au voisinage du centre d'un miroir sphérique. Ces points et leurs images sont symétriques par rapport au centre.

La seconde condition nécessite pour sa part que l'angle \(\alpha\) soit suffisamment petit pour qu'au second ordre près, on puisse écrire \(\cos~\alpha=1\). Dans ce cas en effet, l'équation fondamentale des miroirs sphériques prend la forme simple :

\(\frac{1}{\overline{\mathrm{CA}}}+\frac{1}{\overline{\mathrm{CA'}}}=\frac{2}{\mathrm r}\)

qui exprime, puisque l'angle \(\alpha\) n'y figure plus, que :

Attention :

Le stigmatisme approché est satisfait pour tous les points de l'espace qui n'envoient sur le miroir qu'un pinceau lumineux peu ouvert dont le rayon moyen est normal à la surface réfléchissante.

De façon générale, on voit donc que pour obtenir par réflexion sur un miroir sphérique une image^[3] convenable d'un objet ponctuel, il faut que celui-ci n'émette que des rayons lumineux presque normaux à la surface du miroir; comme ces rayons passent nécessairement au voisinage du centre, ils sont souvent appelés rayons centraux.

Précisons toutefois que les miroirs sphériques étant des surfaces de révolution autour de leur axe principal^[5], ils sont généralement utilisés au voisinage de cet axe. Si l'on prend soin de les faire travailler à faible ouverture, en les diaphragmant par exemple, on obtient ainsi des images approximativement stigmatiques de l'ensemble des points qui appartiennent à leur axe principal ou qui lui sont proches. Les rayons lumineux qui dans ce cas sont voisins de l'axe et peu inclinés par rapport à lui, sont appelés des rayons paraxiaux^[6]. Ce sont eux que nous allons prendre en considération à partir de maintenant; en effet les conclusions auxquelles nous venons d'aboutir nous montrent que :

le stigmatisme approché n'est satisfait de manière très générale que si le miroir sphérique a une faible ouverture et ne reçoit que des rayons paraxiaux des points de la source qui l'éclairent.

Les deux conditions que nous venons d'énoncer constituent les conditions d'approximation de Gauss^[7]. Elles jouent en Optique Géométrique un rôle fondamental car, comme nous aurons l'occasion de le voir, elles sont valables pour tous les systèmes optiques qui possèdent un axe de symétrie de révolution.

Notes

Stigmatisme
Propriété d'un système optique qui associe un seul point image à un seul point source. Un système peut n'être stigmatique que pour certains points remarquables. Pour un système stigmatique, tous les rayons issus d'un point source du domaine de stigmatisme, convergent vers le (ou proviennent du) même point image. Le stigmatisme est dit rigoureux lorsque le chemin optique entre le point objet et le point image est indépendant du rayon. Le stigmatisme est dit approché lorsque les conditions de Gauss sont nécessaires pour qu'il soit réalisé.
Exemple de système non stigmatique pour le couple de points \(AA'\) : le rayon \(APP"A"\) ne passe pas par \(A'\), image de \(A\) par d'autres rayons.
Un dioptre plan n'est pas stigmatique.
Objet
En optique, on appelle objet tout ensemble de points lumineux. Il peut s'agir d'une source primaire qui produit de la lumière (ex : soleil, étoiles, filament de lampe allumée, écran de télévision ou d'ordinateur en fonction), ou d'une source secondaire qui diffuse une partie de la lumière qu'elle reçoit (ex : lune, planètes, la plupart des objets qui nous entourent lorsqu'ils sont éclairés).
On considère, en général, des objets plans situés dans des plans de front de systèmes optiques.
Dans des systèmes composés on pourra considérer qu'une image produite par une première partie du système est un objet pour le reste du système.
Image
On appelle image d'un objet par un système optique, l'ensemble des images des points de l'objet.
On appelle image d'un point, la zone de convergence des rayons, après traversée du système optique (image réelle) ou la zone d'où les rayons semblent provenir (image virtuelle). Lorsque cette zone se réduit à un point, le système est dit stigmatique.
En pratique, l'image ressemble à l'objet (sinon le système ne présente pas d'intérêt), elle peut être
- agrandie : plus grande que l'objet ( |grandissement| >1) ;
- rapetissée : plus petite que l'objet ( |grandissement| <1) ;
- droite : dans le même sens que l'objet (grandissement >0) ;
- renversée : dans le sens contraire à l'objet (grandissement <0) ;
- déformée : un système qui déforme parce qu'il n'a pas le même grandissement dans différentes directions provoque une anamorphose (ex : glace déformante) ;
- floue
Faisceau Lumineux
Un faisceau lumineux est constitué d'un ensemble de rayons.
Il peut être :
- parallèle si les rayons qui le constituent sont parallèles,
- convergent si les rayons qui le constituent, convergent vers un même point
- divergent si les rayons qui le constituent, semblent provenir d'un même point.
Remarque :
Un faisceau convergent devient un faisceau divergent après passage par le point de convergence.
Axe Principal
Étant donné un système optique centré, c'est à dire qui possède un axe de symétrie de révolution, qui traverse l'espace objet réel et l'espace image réelle. On appelle axe principal du système cet axe de symétrie.
Exemple : Lentille convergente.
Contre-exemple : Une lentille cylindrique possède un axe de révolution mais n'est pas un système centré.
Rayons Paraxiaux
Les rayons peu inclinés sur l'axe principal sont appelés rayons paraxiaux.
Lorsqu'on se limite à l'étude de tel rayons, on peut considérer valable l'approximation qui permet de confondre l'angle d'incidence et son sinus (\(a~\approx~\sin~a\)).
On dit alors qu'on travaille dans les conditions de GAUSS.
Dans ces conditions, il y a stigmatisme pour les points objet et image. Ce stigmatisme est dit approché car il nécessite les conditions de Gauss pour être réalisé.
Conditions de GAUSS
Un système est utilisé dans les conditions de Gauss, lorsque les rayons qui le traversent sont peu inclinés sur l'axe principal ( rayons paraxiaux).
On peut alors considérer valable l'approximation qui permet de confondre l'angle d'incidence et son sinus (a~sina).
Dans ces conditions, il y a stigmatisme pour les points objet et image.
Ce stigmatisme est dit approché car il nécessite les conditions de Gauss pour être réalisé.
C'est en 1841 que Gauss a, le premier, présenté un exposé sur la formation des images dans cette approximation. Depuis, on emploie également les termes d'approximation de Gauss ou d'optique Gaussienne.