Formules de conjugaison : Newton (origine en F)
Désignant par : \(\sigma=\overline{\mathrm{FA}}~~~\) \(~~\delta=\overline{\mathrm{FA'}}~~\) et \(~~\mathrm f=\overline{\mathrm{SF}}=\overline{\mathrm{SF'}}=\mathrm{f'}\) ( attention ! ) on obtient :
\(\sigma\sigma'=\mathrm f^2~~~~\) avec \(~~\gamma=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=-\frac{\sigma'}{\mathrm f}=-\frac{\mathrm f}{\sigma}\)
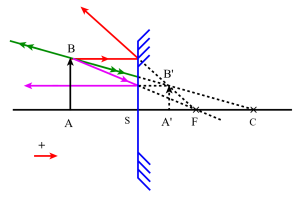
Etablissons ces relations comme précédemment dans le cas d'un miroir convexe et d'un objet réel[1] \(\mathrm{AB}\) :
\(\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{FA'}}}{\overline{\mathrm{FS}}}=-\frac{\overline{\mathrm{FA'}}}{\overline{\mathrm{SF}}}=-\frac{\sigma'}{\mathrm f}\)
\(\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{FS}}}{\overline{\mathrm{FA}}}=-\frac{\overline{\mathrm{SF}}}{\overline{\mathrm{FA}}}=-\frac{\mathrm f}{\sigma}\)
on a donc bien : \(\gamma=-\frac{\sigma'}{\mathrm f}=-\frac{\mathrm f}{\sigma}\) soit : \(~~\sigma\sigma'=\mathrm f^2\)