Miroir Sphérique

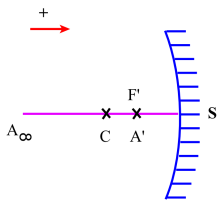
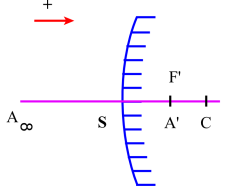
Considérons sur l'axe principal^[1] \(\mathrm{SC}\) d'un miroir sphérique un point source \(\mathrm A\) situé à l'infini.

Par application de la relation (1) il vient, puisque \(\overline{\mathrm{SA}}=\infty\) :

\(\overline{\mathrm{SA'}}=\frac{\mathrm R}{2}=\frac{\overline{\mathrm{SC}}}{2}\)

autrement dit, l'image \(\mathrm{A'}\) de \(\mathrm A\) se situe au milieu du segment \(\mathrm{SC}\).

Ce point que l'on désigne par \(\mathrm{F'}\), est par définition le foyer principal^[2] image du miroir ; il est réel si le miroir est concave, virtuel pour une surface réfléchissante convexe.

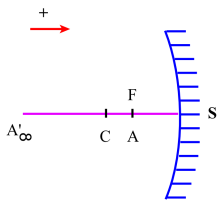
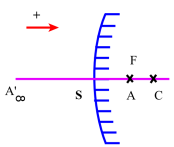
Inversement, on appelle foyer principal objet la position particulière \(\mathrm{F}\) où il faut placer sur l'axe principal d'un miroir sphérique un point source \(\mathrm A\) pour que son image \(\mathrm{A'}\) soit rejetée à l'infini sur cet axe ; comme dans ce cas \(\overline{\mathrm{SA'}}=\infty\) :

\(\overline{\mathrm{SA}}=\frac{\mathrm R}{2}=\frac{\overline{\mathrm{SC}}}{2}\)

avec A réel si le miroir est concave, virtuel s'il est convexe.

En d'autres termes, les deux foyers principaux d'un miroir sphérique sont confondus et de même nature. En outre leur position sur l'axe est parfaitement définie ; on la repère à partir du sommet \(\mathrm S\) en introduisant la notion de distance focale f qui est égale à :

\(\mathrm f=\overline{\mathrm{SF'}}=\overline{\mathrm{SF}}=\frac{\overline{\mathrm{SC}}}{2}=\frac{\mathrm R}{2}\)

On peut facilement vérifier expérimentalement l'existence et la position de ces foyers principaux. Auparavant toutefois il convient de remarquer que lorsqu'une source ponctuelle, située dans un milieu transparent isotrope et homogène, s'éloigne à l'infini dans une direction donnée par rapport au centre d'un système optique^[3], les rayons qu'elle émet tendent tous à devenir, au voisinage du système, parallèles à cette direction.

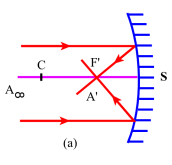
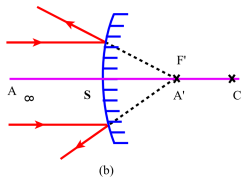
Autrement dit pour mettre en évidence \(\mathrm{F'}\), il suffit de réaliser à l'aide d'un montage optique auxiliaire un pinceau de lumière composé de rayons parallèles à l'axe principal du miroir sphérique.

On observe alors que si le miroir est concave (a) la lumière va effectivement, après réflexion, converger en un point réel \(\mathrm{F'}\) qui se situe bien à mi-distance entre le sommet \(\mathrm S\) et le centre du miroir.. En revanche lorsque la surface réfléchissante est convexe (b), les rayons réfléchis forment un pinceau conique divergent^[4] dont le sommet \(\mathrm{F'}\) ne peut être repéré qu'en traçant au delà du miroir le prolongement de ces rayons ; là aussi on vérifie, pour un miroir dont on connaît le rayon de courbure \(\mathrm R\) que \(\mathrm{F'}\), qui est virtuel, est au milieu du segment \(\mathrm{SC}\).

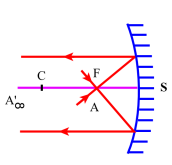
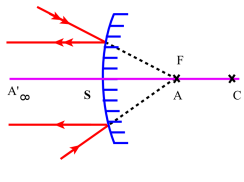
Pour le foyer principal^[2] objet \(\mathrm{F}\), il suffit en s'aidant là encore d'un montage optique auxiliaire, de former sur l'axe principal^[1] du miroir un point lumineux \(\mathrm A\) qui selon la nature du miroir sera réel (a) ou virtuel (b). Dans les deux cas, lorsque \(\mathrm A\) occupe la position de \(\mathrm F\), le pinceau de lumière réfléchie apparaît sous forme d'une nappe cylindrique dont les génératrices sont parallèles à l'axe principal.

On peut remarquer que ces expériences constituent également une illustration du principe du retour inverse de la lumière.

Le foyer principal image du miroir sphérique est illustré par les vidéos suivantes :

La détermination des foyers principaux image du miroir sphérique est illustré par les vidéos suivantes :