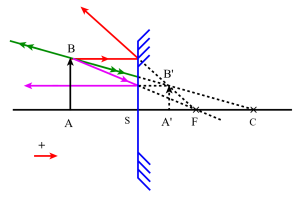
Formules de conjugaison : Descartes (origine en S)
Désignant par : \(\mathrm p=\overline{\mathrm{SA}}~~~~~\) \(\mathrm{p'}=\overline{\mathrm{SA'}}~~~~~\) \(\mathrm f=\overline{\mathrm{SF}}\) on obtient :
\(\frac{1}{\mathrm{p'}}+\frac{1}{\mathrm p}=\frac{1}{\mathrm f}~~~~\) avec \(~~\gamma=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=-\frac{\mathrm{p'}}{\mathrm p}\)
Etablissons ces relations dans le cas d'un miroir convexe, pour un objet réel[1] \(\mathrm{AB}\) par exemple :
\(\frac{\overline{\mathrm{CA'}}}{\overline{\mathrm{CA}}}=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{FA'}}}{\overline{\mathrm{FS}}}~\),
or \(\overline{\mathrm{CA'}}=\overline{\mathrm{CS}}+\overline{\mathrm{SA'}}\)
\(\overline{\mathrm{CA}}=\overline{\mathrm{CS}}+\overline{\mathrm{SA}}\)
\(\overline{\mathrm{FA'}}=\overline{\mathrm{FS}}+\overline{\mathrm{SA'}}\)
en reportant ces valeurs dans la relation qui précède on obtient :
\(\frac{\overline{\mathrm{CS}}+\overline{\mathrm{SA'}}}{\overline{\mathrm{CS}}+\overline{\mathrm{SA}}}=\frac{\overline{\mathrm{FS}}+\overline{\mathrm{SA'}}}{\overline{\mathrm{FS}}}\)
en faisant le produit des moyens et des extrêmes, il vient : \(\frac{1}{\overline{\mathrm{SA}}}+\frac{1}{\overline{\mathrm{SA'}}}=\frac{1}{\overline{\mathrm{SF}}}\)
D'autre part le grandissement[2] transversal vaut : \(\gamma=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{SA'}}}{\overline{\mathrm{AS}}}\)
puisque \(\widehat{ASB}=\widehat{A'SB'}=\mathrm i=\mathrm r\) et donc que les triangles \(\mathrm{SAB}\) et \(\mathrm{SA'B'}\) sont semblables, on retrouve bien : \(\gamma=-\frac{\overline{\mathrm{SA'}}}{\overline{\mathrm{SA}}}\)