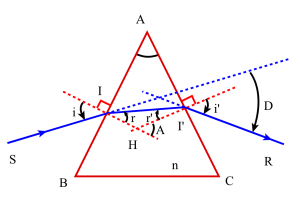
Conditions d'émergence
Pour établir les formules du prisme, nous avons fait l'hypothèse qu'il existait un rayon émergent I'R, mentionnant, à cette occasion, que certaines conditions angulaires devaient être satisfaites.
Examinons donc plus en détail cette question qui est directement liée au phénomène de réfraction.
Simuler
L'animation suivante met en évidence l'existence de conditions pour qu'un rayon incident sur un prisme puisse émerger par l'autre face du prisme :
On sait en effet que lorsqu'un rayon lumineux se propage d'un milieu plus réfringent vers un milieu moins réfringent, il peut être soit réfracté soit totalement réfléchi, selon que son angle d'incidence est inférieur ou non à l'angle limite λ attaché au milieu le plus réfringent
\(\mathrm n~\sin~\lambda=\sin\Big(\pm\frac{\pi}{2}\Big)=\pm1\)
Dans le cas du prisme, cette alternative existe au niveau du rayon intermédiaire II' .
Ainsi, pour qu'il y ait émergence en I' il est nécessaire, compte tenu des conventions de signe adoptées pour définir les angles, que : \(-\frac{\pi}{2}~\le~\mathrm{i'}~\le~+\frac{\pi}{2}~~\), c'est-à-dire : \(-\lambda~\le~\mathrm{r'}~\le~+\lambda\)
Or A= r + r' , soit r' = A - r . Il faut donc que l'on ait : \(-\lambda~\le~\mathrm A-\mathrm r~\le~\lambda~~~~~~(5)\)
Cette double inégalité fait intervenir deux paramètres indépendants :
A qui est lié aux caractéristiques géométriques du prisme
r qui est directement corrélé à l'angle i d'incidence du rayon lumineux.