Influence de l'angle A sur la déviation
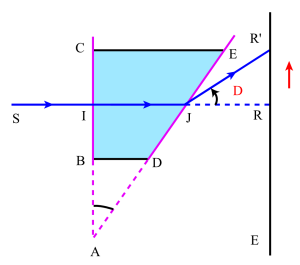
Considérons un prisme matérialisé par une cuve de section BCDE dont les faces opposées BC et DE sont deux glaces transparentes de faible épaisseur, mobiles autour de deux axes passant respectivement par B et D normalement au plan de la figure, ces fenêtres permettent de réaliser un prisme d'angle A variable, dont l'indice constant n est égal à celui du liquide (généralement de l'eau) qui remplit la cuve. On éclaire ce prisme par un pinceau lumineux très étroit dont on fixe, une fois pour toutes, l'angle d'incidence i sur la face d'entrée BC.
De façon à pouvoir ultérieurement apprécier facilement la grandeur de l'angle de déviation D, le plus simple est de choisir i=0 ; dans ces conditions en effet les rayons SI et IJ sont dans le prolongement l'un de l'autre.
Commençons alors par placer la fenêtre DE parallèlement à la face BC. On observe que la lumière vient frapper l'écran E en R ,dans l'alignement de SIJ ; la cuve se comporte en effet ici comme une lame à faces planes et parallèles, cas limite du prisme puisque A=0.
Inclinons maintenant progressivement la fenêtre DE afin d'augmenter continûment la valeur de l'angle A ; sur l'écran la tâche lumineuse évolue, se déplaçant de R vers R'. On peut ainsi noter que ,tant que le rayon intermédiaire IJ n'a pas abordé la face de sortie DE du prisme sous un angle d'incidence au moins égal à l'angle limite correspondant à l'indice du liquide contenu dans la cuve, soit 48° s'il s'agit de l'eau, l'angle de déviation D varie dans le même sens que l'angle A du prisme.
Au delà de cet angle limite, l'expérience s'arrête car le pinceau lumineux est totalement réfléchi à l'intérieur du liquide et la tâche lumineuse disparaît de l'écran E.
Ce résultat expérimental peut faire l'objet d'une interprétation théorique. En effet différencions les formules du prisme en prenant soin de laisser constants n et i ; il vient alors :
\(0 = \mathrm{dr}\)
\(\cos~\mathrm{i'}~.~\mathrm{di'}= \mathrm n~.\cos~\mathrm{r'}~.~\mathrm{dr'}\)
\(\mathrm{dA}=\mathrm{dr'}\)
\(\mathrm{dD}=\mathrm{di'}-\mathrm{dA}\)
qui entraîne :
\(\frac{\mathrm{dD}}{\mathrm{dA}}=\frac{\mathrm{di'}}{\mathrm{dA}}-1=\frac{\mathrm{di'}}{\mathrm{dr'}}-1=\mathrm n~\frac{\cos~\mathrm{r'}}{\cos~\mathrm{i'}}-1\)
Dans cette relation, n est supérieur à 1 ; en outre \(|\mathrm{r'}|<|\mathrm{i'}|\) et donc \(\cos~\mathrm{r'}>\cos~\mathrm{i'}\). Ainsi \(\frac{\mathrm{dD}}{\mathrm{dA}}\) apparaît comme une quantité toujours positive, ce qui conduit bien à la conclusion que :
la déviation D est une fonction croissante de l'angle A du prisme.
Observer
L'animation vidéo suivante montre l'influence de l'angle du prisme A sur la déviation d'un rayon lumineux :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.