Influence de l'indice n sur la déviation
Comme dans le cas précédent, nous allons étudier la variation de la déviation D en fonction de l'indice n par deux approches différentes.
La première consiste à prendre en considération la fonction f qui définit l'angle D par D = f ( A , n , i ) et à rechercher le signe de sa dérivée \(\frac{\mathrm{dD}}{\mathrm{dn}}\) pour A et i constants. La différentiation des formules du prisme nous conduit dans ces conditions aux relations suivantes :
\(0 = \mathrm n~.~\cos~\mathrm r~.~\mathrm{dr} + \sin~\mathrm r~.~\mathrm{dn}~~(1)\)
\(\cos~\mathrm{i'}~.~\mathrm{di'} = \mathrm n~.~\cos~\mathrm{r'}~.~\mathrm{dr'} + \sin~\mathrm{r'}~.~\mathrm{dn}~~(2)\)
\(0 = \mathrm{dr} + \mathrm{dr'}~~(3)\)
\(\mathrm{dD} = \mathrm{di'}~~(4)\)
La résolution de ce système est simple si l'on remarque que (2) peut s'écrire, compte-tenu de (4) et (3) :
\(\cos~\mathrm{i'}~.~\mathrm{dD} = - \mathrm n~.~\cos~\mathrm{r'}~.~\mathrm{dr} + \sin~\mathrm{r'} ~.~\mathrm{dn}~~(5)\)
En effet, l'équation (1) permet d'exprimer dr en fonction de dn, ce qui entraîne pour (5) :
\(\cos~\mathrm{i'}~.~\mathrm{dD}=\Big[\frac{\sin~\mathrm r}{\cos~\mathrm r}~\cos~\mathrm{r'}+\sin~\mathrm{r'}\Big]~\mathrm{dn}~~\) soit
\(\frac{\mathrm{dD}}{\mathrm{dn}}=\frac1{\cos~\mathrm{i'}~.~\cos~\mathrm r}\Big[\sin~\mathrm r~.~\cos~\mathrm{r'}~+~\sin~\mathrm{r'}~.~\cos~\mathrm r\Big]=\frac{\sin~(\mathrm r~+~\mathrm{r'})}{\cos~\mathrm{i'}~.~\cos~\mathrm r}\) ou mieux
\(\frac{\mathrm{dD}}{\mathrm{dn}}=\frac{\sin~\mathrm A}{\cos~\mathrm{i'}~.~\cos~\mathrm r}\)
Cette expression est toujours positive, quel que soit le cas de figure. Il faut donc en conclure que:
la déviation D est une fonction croissante de l'indice n du prisme.
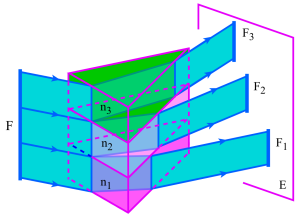
Il existe comme nous l'avons indiqué, une autre démarche pour atteindre ce résultat. Celle-ci ,qui consiste à faire une étude purement expérimentale du phénomène, nécessite de disposer d'un polyprisme. Il s'agit d'un ensemble de plusieurs prismes superposés, de géométrie identique: même angle A, mêmes faces et même arête et dont les indices n1, n2 et n3 ont des valeurs croissantes : n1 > n2 > n3.
Eclairons sous le même angle d'incidence l'ensemble de ces prismes, grâce à un pinceau lumineux monochromatique issu d'une fente source fine F, parallèle à leur arête commune. Si les conditions d'émergence sont satisfaites, on remarque à la sortie du polyprisme une séparation de la lumière en trois pinceaux , repérables sur un écran E par leurs traces F1 , F2 et F3. Celles-ci, qui sont nettement séparées les unes des autres, nous renseignent donc sur la relation qui existe entre le phénomène de déviation et la valeur de l'indice du prisme. En effet, on voit ici clairement que la lumière est d'autant plus déviée que l'indice du prisme qu'elle a traversé, est plus élevé.
En d'autres termes, la déviation varie dans le même sens que l'indice du prisme, toutes choses étant égales par ailleurs.
Observer
Les animations vidéo suivantes montrent l'influence de l'indice du prisme sur la déviation d'un pinceau lumineux :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.