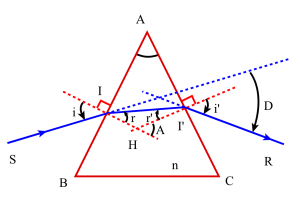
Influence de A sur les conditions d'émergence
Dans la relation (5) qui est équivalente à \(\mathrm r-\lambda~\le~\mathrm A~\) et \(~\mathrm A~\le~\mathrm r+\lambda\)
la première inégalité est toujours satisfaite. En effet quel que soit le cas de figure :
\(\mathrm r~\le~\lambda~\) soit \(~\mathrm r-\lambda~\le~0~\) ; or \(\mathrm A>0\) , sinon le prisme n'existerait pas physiquement.
On vérifie bien que : \(~\mathrm A~\ge~\mathrm r-\lambda\).
Quant à la deuxième inégalité : \(~\mathrm A~\le~\mathrm r+\lambda\) elle entraîne puisque \(\mathrm r~\le~\lambda\) que l'on ait : \(\mathrm A~\le~2\lambda\)
Simuler
L'animation suivante met en évidence l'existence de conditions pour qu'un rayon incident sur un prisme puisse émerger par l'autre face du prisme :