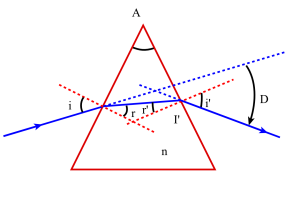
Etude de la déviation
Nous avons vu que lorsqu'un rayon lumineux monochromatique, défini par son angle d'incidence i , arrive sur la face d'entrée d'un prisme d'angle A et d'indice n, il subit à la sortie du prisme, si les conditions d'émergence sont satisfaites, une déviation D dont la valeur est parfaitement déterminée.Nous avons vu que lorsqu'un rayon lumineux monochromatique, défini par son angle d'incidence i , arrive sur la face d'entrée d'un prisme d'angle A et d'indice n, il subit à la sortie du prisme, si les conditions d'émergence sont satisfaites, une déviation D dont la valeur est parfaitement déterminée.
En d'autres termes, D apparaît comme une fonction de A, n et i : D = f ( A, n, i )
Ce résultat peut être précisé à partir des formules du prisme établies précédemment :
\(\sin~i=n~\sin~r\)
\(\sin~i'=n~\sin~r'\)
\(A=r~+~r'\)
\(D=i~+~i'~-~A\)
En effet ces relations constituent un système de 4 équations à 7 inconnues ; pour le résoudre mathématiquement, on sait qu'il est nécessaire de choisir 3 variables quelconques qui seront considérées comme indépendantes. Si l'on retient les grandeurs A , n et i , qui sont directement accessibles à la mesure, il est donc possible de déterminer l'expression de la fonction f et par suite de faire une étude physique exhaustive de la déviation.
Nous allons donc examiner successivement l'influence sur D de ces trois grandeurs indépendantes A , n et i , en veillant à laisser constantes les valeurs des deux paramètres non concernés.