Stigmatisme absolu.
On sait que pour le dioptre plan, le stigmatisme[1] absolu n'est réalisé que pour les seuls points objets qui sont leurs propres images, c'est à dire pour les sources ponctuelles situées à l'infini ou sur la surface du dioptre. Cela signifie que : pour un prisme, l'ensemble des points à l'infini et ceux qui appartiennent à son arête sont rigoureusement stigmatiques.
On doit noter que ces points ne sont pas les seuls pour lesquels il y a stigmatisme absolu. On démontre en effet qu'il existe à distance finie des points sources qui, bien que non stigmatiques pour un dioptre, le sont pour l'ensemble des deux dioptres qui constituent le prisme. La mise en évidence de ces points et celle de leurs images ponctuelles, qui sont elles-mêmes à distance finie, nécessitent une étude qui dépasse le cadre de ce cours. Nous nous contenterons donc d'indiquer ici que ces couples de points rigoureusement stigmatiques se répartissent dans l'espace en fonction de l'angle d'incidence i sous lequel la lumière portée par le rayon moyen issu de ces sources arrive sur la face d'entrée du prisme.
Définition : plans homocentriques
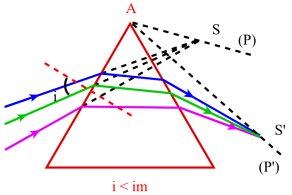
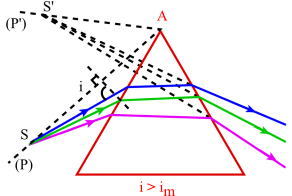
On établit ainsi que pour chaque valeur de i, il existe deux plans conjugués[2] (P) et (P') tel qu'à tout point S de l'un correspond dans le même plan de section principale un point S' de l'autre. Ces plans qui sont appelés plans homocentriques passent tous par l'arête du prisme.
On peut préciser que (P) et (P') sont toujours de nature différente; en outre lorsque l'angle d'incidence i est inférieur à im, angle pour lequel il y a minimum de déviation, (P) est virtuel et donc (P') est réel ; la situation est inverse quand i > im .
Observer
L'animation vidéo suivante montre le stigmatisme des points à l'infini :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.