Influence de i sur les conditions d'émergence

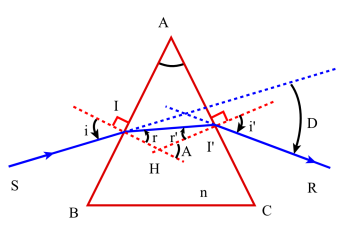
La relation (5) peut s'exprimer également sous la forme de deux autres inéquations :

\(-\mathrm A-\lambda~\le~\mathrm r~~\) soit \(~~\mathrm A+\lambda~\ge~\mathrm r\)

et

\(-\mathrm r~\le~\lambda-\mathrm A~~\) soit \(~~\mathrm r~\ge~\mathrm A-\lambda\)

La première relation est toujours vraie, car \(\lambda~\ge~\mathrm r\) et \(\mathrm A~\ge~\lambda\) ; la seconde en revanche impose que l'angle i d'incidence du rayon lumineux soit tel que :

\(\sin~\mathrm i=\mathrm n~\sin~\mathrm r~\ge~\mathrm n~\sin(\mathrm A-\lambda)\)

ou, ce qui est équivalent, que :

\(\mathrm i~\ge~\mathrm i_0~~\) avec \(~\sin~\mathrm i_0=\mathrm n~\sin(\mathrm A-\lambda)\)

En conclusion,

Pour qu'un rayon lumineux, défini par son angle d'incidence i, émerge d'un prisme d'angle A et d'indice n, il faut que soient satisfaites simultanément les deux conditions d'émergence suivantes :

\(\mathrm A~\le~2\lambda~~\) avec \(~\sin~\lambda=\frac1{\mathrm n}\)

\(\mathrm i~\ge~\mathrm i_0~~\) avec \(~\sin~\mathrm i_0=\mathrm n~\sin(\mathrm A-\lambda)\)

A partir de ces résultats qui ne sont valables que pour des rayons qui se propagent directement entre les faces d'entrée et de sortie du prisme, il est possible de déterminer pour un prisme d'angle A donné l'ouverture maximale du faisceau lumineux[1] incident auquel correspond un faisceau émergent. Il suffit pour cela de tenir compte des conventions de signe définies précédemment pour les angles tels que i, et de faire appel au principe du retour inverse de la lumière pour aboutir aux conclusions suivantes:

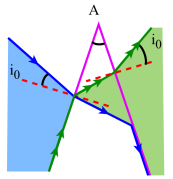
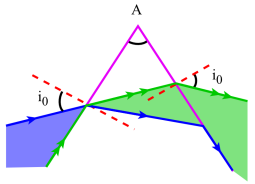
  • il existe deux situations différentes selon que : \(\mathrm A<\lambda\) ou \(\lambda~\le~\mathrm A~\le~2\lambda\)

  • dans le premier cas, faisceaux incident et émergent ont une ouverture supérieure à 90°; certains rayons lumineux sont donc déviés vers l'arête du prisme

  • si \(\lambda~\le~\mathrm A~\le~2\lambda\) ce qui est le cas le plus fréquent, tous les rayons subissent une déviation qui les rabat vers la base du prisme

Observer

L'animation vidéo suivante montre l'influence de l'angle d'incidence i sur les conditions d'émergence :

Influence de l'angle d'incidence sur les conditions d'émergence d'un prisme