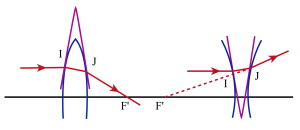
Foyers, plans focaux. Distances focales [Lentilles minces]

Foyers, plans focaux. Distances focales

La lentille mince ^[1]qui est un système centré dioptrique possède deux plans focaux perpendiculaires à l' axe principal ^[2]aux foyers objet F et image F'. Comme les milieux extrêmes sont identiques les distances focales sont égales en valeur absolue et l'on a : \(\overline{\mathrm{OF'}}=\mathrm{f'}=-\overline{\mathrm{OF}}=-\mathrm f\)

On déterminera la valeur de la distance focale ^[3]image à partir de la vergence C d'une lentille épaisse en considérant que : \(\overline{\mathrm S_1\mathrm S_2}\approx0\)

On obtient alors : \(\mathrm C=\frac{\mathrm n_0}{\mathrm{f'}}=(\mathrm n~-~\mathrm n_0)~\Big(\frac1{\overline{\mathrm S_1\mathrm C_1}}~-~\frac1{\overline{\mathrm S_2\mathrm C_2}}\Big)~+~\frac{(\mathrm n~-~\mathrm n_0)^2}{\mathrm n}~\frac{\overline{\mathrm S_1\mathrm S_2}}{\overline{\mathrm S_1\mathrm C_1}~\overline{\mathrm S_2\mathrm C_2}}\)

d'où : \(\mathrm C=(\mathrm n~-~\mathrm n_0)~\Big(\frac1{\overline{\mathrm S_1\mathrm C_1}}~-~\frac1{\overline{\mathrm S_2\mathrm C_2}}\Big)\) où S₁ et S₂ sont confondus avec le point O.

L'expression de la vergence ^[3]C d'une lentille mince permet de montrer qu'il existe deux sortes de lentilles minces :

les lentilles minces convergentes ^[4]pour lesquelles f ' est positive. Le foyer objet ^[5]F est situé dans l'espace objet ^[6]et le foyer image ^[5]F ' est situé dans l' espace image ^[7]; les deux foyers sont réels^[8].
les lentilles minces divergentes ^[4]pour lesquelles f ' est négative et les foyers sont virtuels.

\(\overline{\mathrm{SC}}\) sera compté positivement si la face est convexe et négativement si la face est concave.

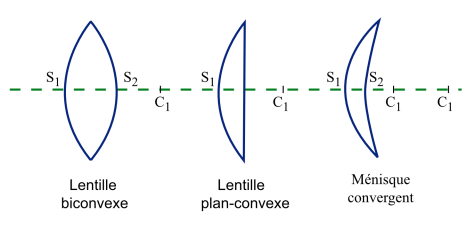
Ainsi la lentille biconvexe, plan convexe ou le ménisque convergent avec \(\overline{\mathrm S_1\mathrm C_1}<\overline{\mathrm S_2\mathrm C_2}\) sont des lentilles convergentes.

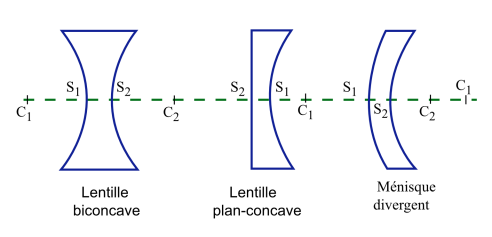
Tandis que la lentille biconcave \(\overline{\mathrm S_1\mathrm C_1}<0\), plan concave \(\overline{\mathrm S_1\mathrm C_1}<0\) ou le ménisque divergent \(\overline{\mathrm S_2\mathrm C_2}<\overline{\mathrm S_1\mathrm C_1}\) sont des lentilles divergentes.

Un rayon incident en I et parallèle à l'axe traverse la lentille suivant IJ et sort en JF'. Entre I et J la lentille se comporte comme un prisme dont les faces seraient les plans tangents en I et J à la lentille ; la base du prisme équivalent est située du côté de l'axe principal^[2].

Les rayons étant déviés du coté de la base du prisme le rayon est rabattu vers l'axe principal. Ainsi une lentille à bords minces sera convergente^[4].

Par contre pour les lentilles à bords épais le prisme équivalent à sa base tournée en dehors de l'axe principal et les rayons s'écartent de l'axe principal : ces lentilles sont divergentes^[4].

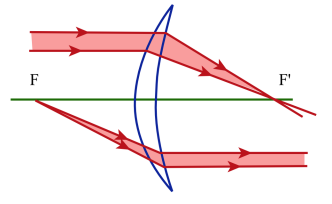
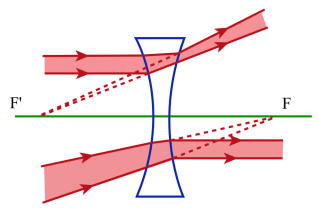
Les lentilles à bords minces sont convergentes.

Les lentilles à bords épais sont divergentes.

Simuler

L'animation suivante présente une classification des lentilles suivant l'épaisseur de leur bord :

Classification des lentilles

Observer

L'animation vidéo suivante montre l'existence du foyer principal image pour une lentille convergente :

Foyer principal image d'une lentille convergente

Les animations vidéo suivantes montrent la convergence ou la divergence d'une lentille selon qu'elle est à bords minces ou épais :

Divergence d'une lentille à bord épais

Convergence d'une lentille à bords minces

Lentille plan-concave et plan-convexe et leur association

Notes

Lentille mince
Une lentille dont l'épaisseur au centre optique est négligeable devant les rayons de courbure des dioptres qui la limitent est dite mince. Dans le cas contraire c'est une lentille épaisse.
Approximation des lentilles minces
Une lentille mince peut être représentée par une lentille infiniment mince lorsqu'on étudie ses propriétés pour des distances [lentille-objet] ou [lentille-image] grandes devant l'épaisseur de la lentille. C'est ce qui est fait dans le cadre de l'optique géométrique élémentaire et en particulier dans l'atelier-schéma.
Axe Principal
Étant donné un système optique centré, c'est à dire qui possède un axe de symétrie de révolution, qui traverse l'espace objet réel et l'espace image réelle. On appelle axe principal du système cet axe de symétrie.
Exemple : Lentille convergente.
Contre-exemple : Une lentille cylindrique possède un axe de révolution mais n'est pas un système centré.
Distance focale d'une lentille
C'est la mesure algébrique de OF' où O est le centre optique et F' le foyer principal image.
Elle est positive pour une lentille convergente.
Puissance intrinseque (ou vergence) d'une lentille
C'est l'inverse de la distance focale exprimée en mètres, elle s'exprime en dioptries.
La puissance intrinseque d'une loupe de (distance) focale 5 cm est de 20 dioptries.
Faisceau Lumineux
Un faisceau lumineux est constitué d'un ensemble de rayons.
Il peut être :
- parallèle si les rayons qui le constituent sont parallèles,
- convergent si les rayons qui le constituent, convergent vers un même point
- divergent si les rayons qui le constituent, semblent provenir d'un même point.
Remarque :
Un faisceau convergent devient un faisceau divergent après passage par le point de convergence.
Foyers
Un foyer image est le point où convergent, après traversée du système optique, les rayons d'un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Un foyer objet est le point d'où partent les rayons qui, après traversée du système optique, forment un faisceau parallèle. Il est dit principal sur l'axe principal, et secondaire en dehors de cet axe.
Dans l'approximation des lentilles minces, l'ensemble des foyers secondaires et le foyer principal sont tous situés dans un plan de front appelé plan focal.
Espace Objet
Espace Objet Réel
L'espace objet réel s'étend en deçà de la face d'entrée du système optique. Un objet situé dans cet espace hachuré est réel : les rayons passent vraiment par le point A.
Espace Objet Virtuel
L'espace objet virtuel s'étend au delà de la face d'entrée du système optique. Un objet situé dans cet espace grisé est virtuel : c'est le prolongement des rayons en aval de la face d'entrée, qui convergent au point A.
Espace Image
Espace Image Réelle
L'espace image réel s'étend au delà de la face de sortie du système optique. Une image située dans cet espace hachuré est réelle. Les rayons y convergent en des points image. L'image réelle peut être observée directement ou bien recueillie sur un écran.
Espace Image Virtuelle
L'espace image virtuel s'étend en deçà de la face de sortie du système optique. Une image située dans cet espace grisé est virtuelle. C'est le prolongement des rayons en amont de la face de sortie, qui semblent venir des points image, une image virtuelle ne peut pas être recueillie sur un écran.
Objet Réel
Un objet réel est un objet situé en avant de la face d'entrée du système optique, dans l'espace objet réel.
Des rayons (bien réel) partent des points qui constituent cet objet vers la face d'entrée du système optique.
Avec une loupe, des lunettes correctrices, ou un télescope, on observe des objets réels.
Dans un système optique composé, une image, formée par une première partie du système, peut être considéré comme un objet réel pour la seconde partie si l'image en question est située en avant de cette seconde partie.