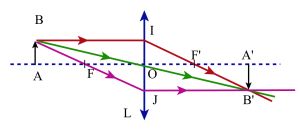
Formules de conjugaison avec origines aux foyers
On a :
\(\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{OI}}}=\frac{\overline{\mathrm{F'A'}}}{\overline{\mathrm{F'O}}}=\frac{\overline{\mathrm{OJ}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{FO}}}{\overline{\mathrm{FA}}}\)
et donc :
\(\overline{\mathrm{FA}}~.~\overline{\mathrm{FA'}}=\overline{\mathrm{OF}}~.~\overline{\mathrm{OF'}}=-\mathrm{f'}^2\)
soit en posant : \(\overline{\mathrm{FA}}=\mathrm x~\) et \(~\overline{\mathrm{F'A'}}=\mathrm{x'}\)
\(\mathrm x~.~\mathrm{x'}=-\mathrm{f'}^2\)
on a également :
\(\frac{\overline{\mathrm{OJ}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{FO}}}{\overline{\mathrm{FA}}}=\frac{\mathrm{f'}}{\mathrm x}\)
\(\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{OI}}}=\frac{\overline{\mathrm{A'B'}}}{\overline{\mathrm{AB}}}=\frac{\overline{\mathrm{F'A'}}}{\overline{\mathrm{F'O}}}=-\frac{\mathrm{x'}}{\mathrm{f'}}\)
on en déduit la formule du grandissement [1]linéaire : \(\gamma=\frac{\mathrm{f'}}{\mathrm x}=-\frac{\mathrm{x'}}{\mathrm{f'}}\)