Formules de Lagrange-Helmholtz
Formules de Lagrange-Helmholtz
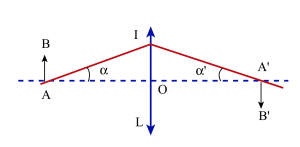
Le rayon AI admet IA' comme rayon conjugué et on peut écrire dans les conditions de Gauss [1]:
\(\overline{\mathrm{OI}}=\alpha.\overline{\mathrm{OA}}=\alpha\mathrm'.\overline{\mathrm{OA'}}\)
soit :
\(\alpha.\mathrm{p}=\alpha'.\mathrm{p'}\)
et \(\frac{\alpha\mathrm'}{\alpha}=\frac{\mathrm p}{\mathrm{p'}}=\frac{\overline{\mathrm{AB}}}{\overline{\mathrm{A'B'}}}\)
d'où la formule de Lagrange-Helmholtz : \(\alpha.\overline{\mathrm{AB}}=\alpha\mathrm'.\overline{\mathrm{A'B'}}\)
Le grandissement [2]axial est défini par : \(~\mathrm g=\frac{\mathrm{dp'}}{\mathrm{dp}}~\) où dp' est le déplacement de l' image [3]correspondant à un déplacement dp très petit de l' objet [4].
En reprenant la relation : \(-\frac1{\mathrm p}+\frac1{\mathrm{p'}}=\frac1{\mathrm{f'}}\) et en la différentiant on obtient :
\(\frac{\mathrm{dp'}}{\mathrm{p'}^2}-\frac{\mathrm{dp}}{\mathrm p^2}=0\)
d'où \(~~\mathrm g=\frac{\mathrm{dp'}}{\mathrm{dp}}=\frac{\mathrm{p'}^2}{\mathrm p^2}=\gamma^2\)