Aire balayée par un vecteur
Durée : 8 mn
Note maximale : 8
Question
Dans un repère orthonormé direct \((O, x, y, z)\) un point \(M\) est repéré par ses coordonnées sphériques \(r\), \(\theta\), \(\varphi\).
Calculez l'élément d'aire \(dS\) balayée par le vecteur \(\vec{OM}\) lorsque les coordonnées angulaires \(\theta\) et \(\varphi\) subissent des accroissements \(d\theta\) et \(d\varphi\).
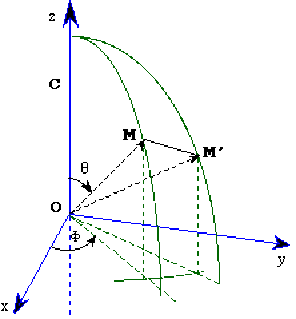
Vérifiez que le résultat s'exprime au moyen d'un produit vectoriel.
Précisez la valeur \(d\delta\) de l'angle \((\vec{OM}.\vec{OM'})\) et la direction de l'axe de rotation autour duquel \(\vec{OM}\) a effectué une rotation d'amplitude \(d\delta\).
Solution
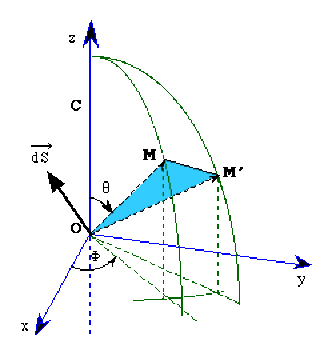
L'aire \(dS\) du triangle \(OMM'\) est la moitié de l'aire du rectangle de côtés \(OM\) et \(MM'\).
On a \(OM=r\) et \(MM'=r\sqrt{d\theta^2+\sin^2\theta d\varphi^2}\).
(2 points)
Donc \(\displaystyle{dS=r^2\frac{d\delta}{2}}\) si on écrit \(MM' =r d\delta\)
avec \(d\delta=(\vec{OM}.\vec{OM'})\).
(1 point)
On vérifie que \(dS=||\frac{1}{2}\vec{OM}\wedge\vec{OM}||=\frac{1}{2}r^2||(d\theta\vec{u_\varphi}-\sin\theta d\varphi\vec{u_\theta} )|||\).
(2 points)
On en déduit que l'axe de rotation est dirigé suivant le vecteur \(d\theta\vec{u_\varphi}-\sin\theta d\theta\vec{u_\theta}\) qui est la projection orthogonale à \(OM\) de la somme des vecteurs \(d\varphi\vec{u_z}\) et \(d\theta\vec{u_\varphi}\) associés aux rotations élémentaires d'angles \(d\varphi\) et \(d\theta\).
(3 points)