Sinus de la somme de deux angles
Durée : 7 mn
Note maximale : 7
Question
On sait que le produit vectoriel de deux vecteurs dépend du sinus de l'angle que forment les axes orientés qui les portent.
Utilisez ce résultat pour retrouver la formule de trigonométrie exprimant \(\sin(a + b)\) où \(a\) et \(b\) sont les valeurs algébriques de deux angles orientés.
Solution
On considère deux vecteurs unitaires,\(\vec{OA}\) et \(\vec{OB}\), dont les extrémités \(A\) et \(B\) sont situées sur le cercle trigonométrique de rayon \(R = 1\).
On a, dans ces conditions :
\(\vec{OA}\wedge\vec{OB}=\sin (\vec{OA}\wedge\vec{OB})\vec{u_z}\)
(1 point)
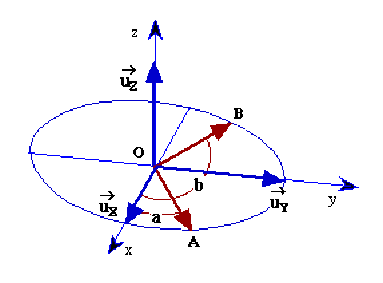
Par rapport au repère orthonormé \((O:\vec{u_x}, \vec{u_y}, \vec{u_z})\) tel que le cercle est dans le plan \((O, x, y)\), on peut écrire :
\(\vec{OA}=\cos a\vec{u_x}+\sin a\vec{u_y}\) et \(\vec{OB}=\cos b\vec{u_x}+\sin b\vec{u_y}\)
(2 points)
On en déduit que \(\vec{OA}\wedge\vec{OB}=(\cos a\sin b -\sin a\cos b)\vec{u_z}\)
(1 point)
Comme, d'autre part, les angles orientés sont liés par la relation,
\(\vec{OA}.\vec{OB}=(\vec{OA}.\vec{u_x})+(\vec{u_x}.\vec{OB})=b - a\)
on trouve finalement :
\(\sin (b - a) = \cos a\sin b-\sin a\cos b\)
(2 points)
et en changeant le signe de a :
\(\sin (b + a) = \cos a\sin b + \sin a\cos b\)
(1 point)