Système 2 masses - 3 Ressorts
Partie
Question
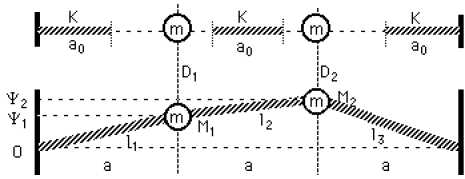
Les deux masses sont assujetties à se déplacer respectivement le long des tiges parallèles \(D_1\) et \(D_2\), disposées horizontalement, qui leur assurent un guidage transversal sans frottement. On notera \(L=3.a\) la longueur totale du système.
Dessiner le système au repos, en représentant les forces agissant sur les masses \(m\).
Appliquer à chacune de ces masses le principe fondamental de la dynamique.
On se place dans le cas de petites oscillations, i.e les amplitudes de vibration \(\psi_1(t)\) resp.\(\psi_2(t)\) des masses situées en \(M_1\) resp. \(M_2\), restent petites devant \(a\).
Montrer qu'alors : \(l_1\simeq l_2\simeq l_3\simeq a\) au second ordre près, d'où l'on déduira que la norme des forces exercées par les ressorts varie assez peu pour pouvoir être considérée comme constante.
Montrer qu'alors les équations du mouvement peuvent s'exprimer par : \(\ddot{\psi}^1=\omega_0^2 . (-2\psi^1+\psi^2), \ddot{\psi}^2=\omega_0^2(\psi^1-2\psi^2)\) avec \(\omega_0^2 =\frac{K}{m}[1-\frac{a_0}{a}]\) et peuvent se résoudre en faisant le changement de coordonnées : \(\phi^1=\frac{\psi^1+\psi^2}{2}\), \(\phi^2=\frac{\psi^1+\psi^2}{2}\)
Exprimer la solution en coordonnées \(\phi^1\) et \(\phi^2\). En déduire \(\psi^1\) et \(\psi^2\) ainsi que la vibration générale du système.
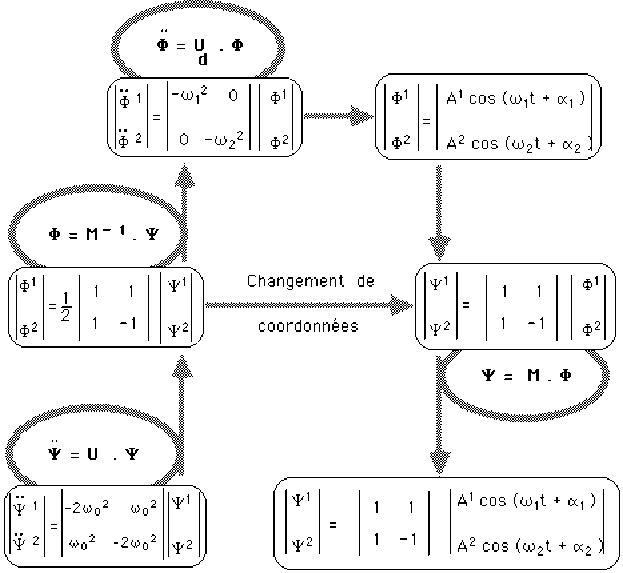
Compléter le tableau Récapitulatif
Aide simple
Revoir la mise en équation : les écarts des masses par rapport à leur position d'équilibre doivent impérativement être représentés algébriquement.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Remarquer sur ces animations que les 2 masses se situent sur une enveloppe sinusoïdale, à l'intersection avec les droites \(D_1\) respectivement \(D_2\).
La période spatiale du mode 1 (symétrique) est égale à \(2.L\).
La période spatiale du mode 2 (antisymétrique) est égale à \(L\).
Rappel de cours
Voir la page Mise en équations
Solution détaillée
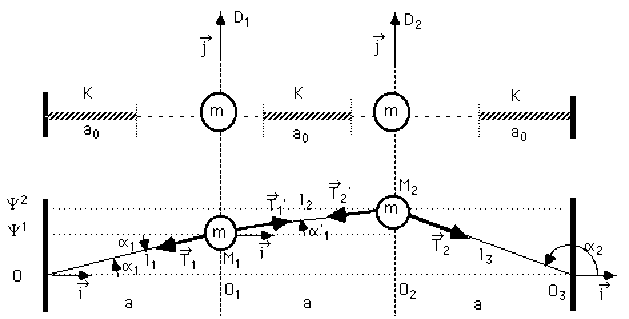
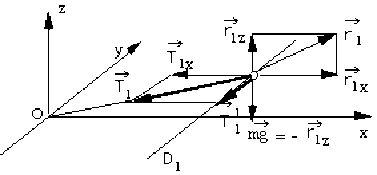
Les masses \(M_1\) et \(M_2\) sont assujetties à se déplacer respectivement le long des tiges parallèles \(D_1\) et \(D_2\).
\(D_1\) et \(D_2\) sont disposées horizontalement \(\Rightarrow\) le poids est orthogonal aux tiges, donc au mouvement. Le poids sera compensé par la composante verticale \(\overrightarrow{r_{1z}}\) de la réaction \(\overrightarrow{r_1}\) de la tige.
\(\Rightarrow\) les composantes verticales des forces s'annulent.
Chaque ressort exerce sur la masse considérée une force située dans le plan horizontal (plan du mouvement). Cette force a 2 composantes : l'une orthogonale à la tige, l'autre sur la tige.
La composante orthogonale à la tige n'intervient pas dans le mouvement : tout au plus pourrait-elle déformer la tige si la tige n'était pas assez rigide, mais ce cas n'est pas envisagé.
Par exemple, la force de tension \(\overrightarrow{T_1}\) a une composante \(\overrightarrow{T_{1x}}\) orthogonale à la tige, compensée par la composante \(\overrightarrow{r_{1x}}\) de la réaction de la tige Le guidage (exercé par les tiges) est sans frottement \(\Rightarrow\) la réaction de chaque tige sur la masse correspondante est orthogonale à la tige.
En résumé, la réaction \(\overrightarrow{r_1}\) de la tige a 2 composantes orthogonales à la tige : \(\overrightarrow{r_{1z}}\) qui compense le poids et \(\overrightarrow{r_{1x}}\) qui compense la composante orthogonale à la tige de la force exercée par le ressort.
On peut faire évidemment le même raisonnement pour chacune des masses et pour chacun des ressorts.
seules sont actives les composantes sur \(D_1\) et \(D_2\) des forces exercées par les ressorts sur les masses \(M_1\) et \(M_2\). (les composantes de toutes les forces qui ne sont par parallèles à \(\overrightarrow j\) s'annulent).
Position du problème.
On doit écrire le principe fondamental de la dynamique en projection sur \(\overrightarrow j\).
Pour exprimer les vecteurs forces, il faut déterminer leur orientation et leur module (et donc les allongements des ressorts).
La tension exercée par un ressort (sous réserve de ne pas trop le comprimer ou de ne pas trop tirer dessus) est proportionnelle à son allongement. Si on appelle \(l\) sa longueur et \(a_0\) sa longueur au repos, la tension vaut : \(K | l-a_0|.\)
Les allongements des ressorts doivent être considérés par rapport à leur longueur au repos (notée \(a_0\)) et non pas par rapport à l'équilibre, car à l'équilibre (\(O\), \(M_1\), \(M_2\), \(O_3\) alignés) les ressorts ont déjà un allongement (\(a>a_0\)).
Les orientations des forces (indiquées sur le schéma) correspondent à ce cas de figure où les ressorts sont toujours étirés ( \(a>a_0\) ). Il faut garder présent à l'esprit le fait que les ressorts sont toujours étirés, ce qui indique le sens des forces qu'ils exercent, et permet de contrôler les valeurs algébriques de leurs composantes.
Pour exprimer les projections des forces sur \(\overrightarrow j\), le sens d'orientation des angles qui interviennent est le sens trigonométrique. Il faut définir tous les angles algébriquement par rapport à ce sens de référence.
On notera ici les angles algébriques : \(\alpha_1=(\overrightarrow i, \overrightarrow{OM_1})\), \(\alpha'_1=(\overrightarrow i, \overrightarrow{M_1M_2})\), \(\alpha_2=(\overrightarrow i, \overrightarrow{OM_2})\).
On utilisera les notations matricielles : l'indice (en bas) désigne un vecteur, les exposants (en haut) désignent les composantes. (Si on doit écrire une expression à la puissance \(n\), on mettra cette expression entre parenthèses pour éviter les confusions de notations).
Projections des forces sur \(\overrightarrow j\)
On obtient :
\(T^1=\overrightarrow j\overrightarrow{T_1}=||\overrightarrow{T_1}||\cos(\overrightarrow j\overrightarrow{T_1})=||\overrightarrow{T_1}||\cos(\frac{\pi}{2}-\alpha_1)= -||\overrightarrow{T_1}||\sin(\alpha_1)=-||\overrightarrow{T_1}||\frac{\psi^1}{l_1}\) \(T'^1=\overrightarrow j\overrightarrow{T'_1}=||\overrightarrow{T'_1}||\cos(\overrightarrow j\overrightarrow{T'_1})=||\overrightarrow{T'_1}||\cos(-\frac{\pi}{2}+\alpha'_1)=||\overrightarrow{T'_1}|| \sin(\alpha'_1)=||\overrightarrow{T'_1}||\frac{\psi^2-\psi^1}{l_2}\)
\(\overrightarrow{T'_2}=- \overrightarrow{T'_1}\Rightarrow T'^2=-T'^1\) (composantes algébriques)
\(T^2=\overrightarrow j\overrightarrow{T_2}=||\overrightarrow{T_2}||\cos(\overrightarrow j\overrightarrow{T_2})=||\overrightarrow{T_2}||\sin(\alpha_2)=||\overrightarrow{T_2}||\frac{\psi^2}{l_3}\)
Le PFD en projection sur \(\overrightarrow j\) donne donc,
pour la masse \(M_1\) : \(T^1+T'^1=||\overrightarrow{T_1}||\frac{\psi^1}{l_1}+||\overrightarrow{T'_1}||\frac{\psi^2-\psi^1}{l_2}=m\ddot{\psi}^1 (1)\)
pour la masse \(M_2\) : \(T^2+T'^2=||\overrightarrow{T'_1}||\frac{\psi^1-\psi^2}{l_2}-||\overrightarrow{T_2}||\frac{\psi^2}{l_3}=m\ddot{\psi}^2 (2)\)
Dans le cas de petites oscillations, les amplitudes des vibrations transversales des masses restent petites devant a.
\((l_1)^2=(a)^2+(\psi^1)^2\Rightarrow l_1=a(1+(\frac{\psi^1}{a})^2)^{1/2}\)
Mais : \((1+\varepsilon)^m=1+m.\varepsilon+O(\varepsilon^2)\) où \(O(\varepsilon^2)\) est infiniment petit de l'ordre de \(\varepsilon^2\).
D'où : \((1+(\frac{\psi^1}{a})^2)^{1/2}\cong(1+\frac{1}{2}(\frac{\psi^1}{a})^2)\) en ne retenant que le premier terme du développement.
Ce terme étant lui-même d'ordre 2, on peut le négliger ici (petites oscillations : \(\psi \ll a\)).
Par conséquent : \(l_1\cong a(1+\frac{1}{2}(\frac{\psi^1}{a})^2)\cong a\) (au second ordre près). De même \(l_2\simeq a, l_3\simeq a\).
Dans l'approximation des petites oscillations transversales, on a donc : \((l_1-a)\simeq(l_2-a)\simeq(l_3-a)\simeq0\)
Comme les allongements respectifs des ressorts peuvent s'écrire en fonction de \((a - a_0)\) par :
\(l_1-a_0=(l_1-a)+(a-a_0) ; l_2-a_0=(l_2-a)+(a-a_0) ; l_3-a_0=(l_3-a)+(a-a_0)\)
on en déduit : \(l_1-a_0\simeq l_2-a_0\simeq l_3-a_0\simeq(a-a_0)\)
D'où : \(||\overrightarrow{T_1}||\cong||\overrightarrow{T'_1}||\cong||\overrightarrow{T'_2}||\cong||\overrightarrow{T_2}||\cong K(a-a_0)\) avec \(a<a_0\)
La norme des forces exercées par les ressorts varie donc assez peu pour pouvoir être considérée comme constante.
Dans ces conditions, les relations (1) et (2) pour les deux masses deviennent : \(T^1+T'^1=-K(a-a_0)\frac{\psi^1}{a}+K(a-a_0)\frac{\psi^2-\psi^1}{a}=m\ddot{\psi}^1\) \(T'^2+T^2=K(a-a_0)\frac{\psi^1-\psi^2}{a}-K(a-a_0)\frac{\psi^2}{a}=m\ddot{\psi}^2\) \(\frac{K(a-a_0)}{m.a}\) étant homogène au carré d'une pulsation, on pose : \(\frac{K(a-a_0)}{m.a}=\omega_0^2\).
On obtient alors : \(\begin{array}{ll} \ddot{\psi}^1=\omega_0^2(-2\psi^1+\psi^2)& (3) \\ \ddot{\psi}^2=\omega^2_0(\psi^1-2\psi^2)& (4) \end{array}\)
Noter que \(\psi =\left|\begin{array}{l} \psi^1 \\ \psi^2 \end{array} \right|\) représente le vecteur d'état du système et \(\ddot{\psi}=\left|\begin{array}{l} \ddot{\psi}^1 \\ \ddot{\psi}^2 \end{array} \right|\) sa dérivée seconde par rapport au temps.
Les équations (3) et (4) peuvent alors s'exprimer sous forme matricielle : \(\ddot{\psi}=\omega_0^2 \left(\begin{array}{cc} -2 & 1 \\ 1 & -2 \end{array} \right)\psi\)
et en posant : \(U=\omega_0^2\left(\begin{array} {cc}-2& 1 \\ 1&-2\end{array} \right)\) matrice du système \(\Rightarrow \ddot{\psi}=U\psi\)
Pour résoudre ce système, on peut soit appliquer le changement de variable qui est proposé dans l'exercice, soit appliquer la méthode générale.
En effectuant le changement de variables : \(\phi^1=\frac{\psi^1+\psi^2}{2} \quad \phi^2=\frac{\psi1-\psi^2}{2}\)
\((3)+(4) \Rightarrow \ddot{\psi}^1+\ddot{\psi}^2=\omega_0^2(-\psi^1-\psi^2) \Rightarrow \ddot{\phi}^1 = -\omega_0^2\phi^1 \quad(5)\)
\((3)-(4) \Rightarrow \ddot{\psi}^1-\ddot{\psi}^2=\omega_0^2(-3\psi^1+3\psi^2) \Rightarrow \ddot{\phi}^2 = -3\omega_0^2\phi^2 \quad (6)\)
On peut maintenant résoudre ces équations (5) et (6), car les coordonnées \(\phi\) sont découplées, contrairement aux équations (3) et (4) où les coordonnées sont \(\psi\) couplées (c'est à dire que \(\ddot{\psi}^1\), accélération de la masse 1, dépend non seulement de la position \(\psi^1\) de la masse 1 mais aussi de la position \(\psi^2\) de la masse 2).
\((5) \quad\Rightarrow \phi^1=A^1\cos(\omega_1t+a_1)\) avec \(\omega_1=\omega_0\)
\((6) \quad\Rightarrow \phi^2=A^2\cos(\omega_2t+a_2)\) avec \(\omega_2=\sqrt3 . \omega_0\)
\(\phi^1=\frac{\psi^1+\psi^2}{2} \Rightarrow \psi^1=\phi^1+\phi^2\)
\(\phi^2=\frac{\psi^1-\psi^2}{2} \Rightarrow \psi^2=\phi^1-\phi^2\) soit : \(\psi =M \phi\) avec \(M=\left(\begin{array} {cc} 1 & 1 \\ 1 & -1 \end{array}\right)\)
et : \(\phi=\left|\begin{array} {ll} \phi^1 \\\phi^2 \end{array}\right| \quad \psi=\left|\begin{array} {ll} \psi^1 \\ \psi^2 \end{array}\right|\)
Remarque : \(M\) est une matrice de changement de base.
Le changement de base inverse est : \(M^{-1}=\frac{1}{2} \left(\begin{array} {cc} 1&1 \\ 1&-1 \end{array}\right)\) et on vérifie que : \(M.M^{-1}=\left(\begin{array} {cc} 1&0 \\ 0&1 \end{array}\right)\)
Ce qui signifie qu'en appliquant successivement un changement de base et le changement de base inverse, on ne change rien (le produit des deux est une matrice unité). On en déduit les solutions en coordonnées \(\psi\) :
\(\psi=\left|\begin{array} {cc} \psi^1 \\\psi^2 \end{array}\right| \quad =M\left|\begin{array} {cc} \phi^1 \\ \phi^2 \end{array}\right|=\left(\begin{array} {cc} 1&1 \\ 1&-1 \end{array}\right) \left|\begin{array} {cc} A^1\cos(\omega_1t+\alpha_1) \\A^2\cos(\omega_2t+\alpha_2) \end{array}\right| =\left|\begin{array} {cc} A^1\cos(\omega_1t+\alpha_1)+A^2\cos(\omega_2t+\alpha_2) \\A^1\cos(\omega_1t+\alpha_1)-A^2\cos(\omega_2t+\alpha_2) \end{array}\right|\) que l'on peut écrire sous la forme d'une combinaison linéaire des modes propres 1 et 2 :
\(\psi =\left|\begin{array}{c} 1 \\ 1 \end{array}\right|A^1\cos(\omega_1t+\alpha_1)+\left|\begin{array}{c} 1 \\ -1 \end{array}\right|A^2\cos(\omega_2t+\alpha_2)= \overrightarrow{\psi_1}+\overrightarrow{\psi_2}\)
La matrice \(M\) est la matrice des directions propres : \(M = ( M_1 , M_2)\) avec
\(M_1=\left|\begin{array}{c} 1 \\ 1 \end{array}\right|\) et \(M_2=\left|\begin{array}{c} 1 \\- 1 \end{array}\right|\)
et les modes propres s'expriment : \(\psi_1=M_1\phi^1\) et \(\psi_2=M_2\phi^2\)
La vibration peut toujours s'exprimer sur la base des modes propres de vibration \(\psi_i\) , soit ici :
\(\psi = M.\phi = M_1 \phi^1 + M_2 \phi^2 = \psi_1+ \psi_2\)
Dans le cas général on ne donne pas, comme on l'a fait ici, le changement de base qui permet le passage des coordonnées \(\psi\) aux coordonnées \(\phi\) où le système est diagonal.
Il est donc nécessaire de le déterminer par la technique générale de recherche des directions propres et valeurs propres d'une matrice. C'est que nous allons faire maintenant.
On repart de l'équation du système : \(\ddot{\psi}=U\psi\) dans laquelle : \(U =\omega_0^2 \left|\begin{array} {cc}-2&1 \\ 1&-2\end{array}\right|\)
On la résout en exprimant que les solutions satisfont la relation : \(\textrm{d\'et}(U + \omega^2 I) = 0\)
où l'on note \(I\) la matrice unité : \(I=\left|\begin{array} {cc}1&0 \\ 0&1\end{array}\right|\)
On pose : \(\omega=\omega_0 \Omega\), où \(\Omega\) est un nombre sans dimension, que l'on peut appeler " pulsation réduite", car il représente la pulsation \(\omega\) en prenant \(\omega_0\) comme unité. \(\Rightarrow \textrm{d\'et}(U+\omega^2I)=\omega^2_0.\textrm{d\'et}\left|\begin{array} {cc}-2+\Omega^2&1 \\ 1&-2+\Omega^2\end{array}\right|=0\)
\(\textrm{d\'et}\left|\begin{array} {cc}-2+\Omega^2&1 \\ 1&-2+\Omega^2\end{array}\right|=0 \Leftrightarrow(\Omega^2-r)^2=0\)
solution \((\Omega^2-r)<0\Rightarrow \Omega^2-r=-1\Rightarrow \Omega^2=1\Rightarrow \omega_1=\omega_0\)
solution \((\Omega^2-r)>0\Rightarrow \Omega^2-r=1\Rightarrow \Omega^2=3\Rightarrow \omega_2=\sqrt3\omega_0\)
\(\ddot{\psi}=U\psi\Rightarrow \ddot{\psi}=UM\phi\)
\(\psi=M\phi\)
\(\Downarrow\)
\(\ddot{\psi}=M\ddot{\phi} \qquad UM_1=-\omega_1^2M_1\)
\(\Downarrow \qquad \ddot{\phi}=U_d\phi\Rightarrow UM\phi=MU_d\phi\Rightarrow UM=MU_d\) \(\ddot{\psi}=MU_d\phi \qquad UM_2=-\omega_2^2M_2\)
\(M_1\) et \(M_2\) sont les "directions propres" de la matrice \(U\), avec pour valeurs propres \(- \omega_1^2\) et \(- \omega_2^2\) respectivement. On résout l'équation : \(U.M_i = - \omega_i^2. M_i\) ou, ce qui revient au même : \(\left(\begin{array} {cc} -2&-1 \\ 1&-2 \end{array}\right) M_i=-\Omega_i^2M_i\)
\(\left(\begin{array} {cc} -2&-1 \\ 1&-2 \end{array}\right) \left(\begin{array} {cc} M_1^1 \\ M_1^2 \end{array}\right) = \Omega_1^2=1 \qquad \Rightarrow M_1^2=M_1^1\)
\(\left(\begin{array} {cc} -2&1 \\ 1&-2 \end{array}\right) \left(\begin{array} {cc} M_1^1 \\ M_1^2 \end{array}\right) = \Omega_1^2=1 \qquad \Rightarrow M_2^2=-M_2^1\)
On rappelle que l'indice (en bas) désigne le vecteur d'état du système et que les modes propres de vibration s'expriment : \(\psi_1 = M_1 \phi^1\) et \(\psi_2 = M_2 \phi^2\)
\(M_1^2=M_1^1 \Leftrightarrow\) dans le mode propre 1 de vibration, l'amplitude \(M_1^1\) de la masse 1 est égale à l'amplitude \(M_1^2\) de la masse 2. (mode symétrique) et toutes les masses vibrent selon la fonction \(\phi^1\) .
\(M_2^2=-M_2^1 \Leftrightarrow\) dans le mode propre 2 de vibration, l'amplitude \(M_2^2\) de la masse 2 est l'opposée de l'amplitude \(M_2^1\) de la masse 1. (mode antisymétrique) et toutes les masses vibrent selon la fonction \(\phi^2\).
Remarque : on dit que \(M_1\) et \(M_2\) sont les "directions propres" de la matrice \(U\) car tout vecteur qui est proportionnel respectivement à \(M_1\) et \(M_2\) est solution de l'équation (l'équation matricielle est linéaire), autrement dit, un mode propre est défini à un coefficient multiplicatif près. Le résultat trouvé ici est bien conforme au résultat particulier qui a été obtenu directement par changement de variable : \(M_1=\left|\begin{array}{c} 1 \\ 1 \end{array} \right|\) et \(M_2=\left|\begin{array}{c} 1 \\- 1 \end{array} \right|\)
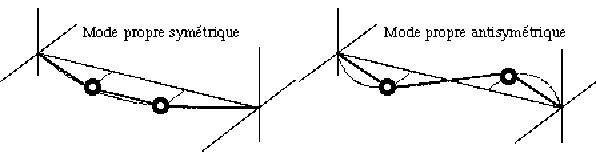
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Remarquer sur ces animations que les 2 masses se situent sur une enveloppe sinusoïdale, à l'intersection avec les droites \(D_1\) respectivement \(D_2\).
La période spatiale du mode 1 (symétrique) est égale à 2.L.
La période spatiale du mode 2 (antisymétrique) est égale à L.
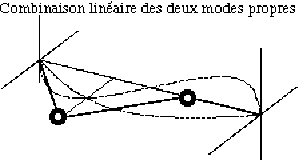
L'état de vibration représenté dans cette animation est la somme des modes (1) et (2).
À l'instant considéré, la masse 1 a une amplitude double de celle dans chacun des modes (\(1 + 1 = 2\)) et la masse 2 a une amplitude nulle (\(1 - 1 = 0\)).
Tableau récapitulatif :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.