Système 2 condensateurs, 2 selfs
Partie
Question
Dans ce système couplé, les selfs ont le même coefficient d'inductance \(L\) et les condensateurs ont la même capacité \(C\).
Ecrire les équations différentielles reliant \(q^1(t)\) et \(q^2(t)\) et leurs dérivées.
Mettre ce système sous forme matricielle et le résoudre
Aide simple
La mise en équation de ce système électrique est analogue à celle du système 2 masses - 2 ressorts.
Repérer les variables analogues de ces deux systèmes.
Rappel de cours
Voir la page Mise en équations
Solution détaillée
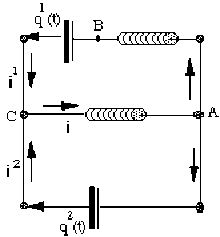
Système 2 Condensateurs, 2 selfs.
Avec les sens >0 choisis, on a :
\(i^1=-\frac{d}{dt}(q^1)=(q^1)'\)
\(i^2=-(q^2)'\)
\(i^3=i^1+i^2=-((q^1)'+(q^2)')\)
On rappelle que pour une self :
\(e=-L\frac{di}{dt}=V_{\textrm{sortie}}-V_{\textrm{entr\'ee}}\)
(par rapport au sens de parcours)
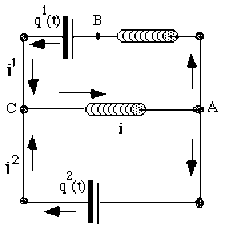
\(\begin{array}{l}V_C-V_B=\frac{q^1}{C} \\V_B-V_A=-L\frac{di^1}{dt}+L(q^1)''\end{array} \quad\Rightarrow V_C-V_A=\frac{q^1}{C}+L(q^1)''\quad (1)\)
\(V_C-V_B=\frac{q^2}{C} \quad (2)\)
\(V_C-V_B=V_{\textrm{entr\'ee}}-V_{\textrm{sortie}}=+L\frac{di}{dt} \quad \Rightarrow V_C-V_A=-L((q^1)''+(q^2)'') \quad (3)\)
(Branche milieu) noeud en C, \(i=i^1+i^2\)
(1) et (2) \(\Rightarrow L(q^1)''=(-\frac{q^1}{C}+\frac{q^2}{C}) \quad \Rightarrow (q^1)''=\frac{1}{LC}(-q^1+q^2) \quad (4)\)
\(\begin{array}{lll}-L(q^2)''-L(q^1)''=(+\frac{q^1}{C}-\frac{q^2}{C})-L(q^2)''&=V_C-V_A&=\frac{q^2}{C} \\ &\Downarrow &\Downarrow\\&(3) &(2)\end{array}\)
\(\Rightarrow L(q^2)''=\frac{1}{C}(q^1-2q^2) \Rightarrow (q^2)''=\frac{1}{LC}(q^1-2q^2)\)
\(\Rightarrow \left(\begin{array}{c} {q^1}'' \\ {q^2}''\end{array} \right)=\frac{1}{LC}\left(\begin{array}{cc} -1&1\\ 1&-2\end{array} \right)\left(\begin{array}{c} q^1 \\ q^2\end{array} \right)\)
à une permutation de ligne et de colonne près ( qui ne change rien ), on retrouve la matrice \(U\) du système 2 masses 2 ressorts
On pose : \(\psi=\left(\begin{array}{c} q^1 \\ q^2\end{array} \right)\)
On pose : \(\omega_0=\frac{1}{LC} \Rightarrow U=\omega_0^2\left(\begin{array}{cc} -1&1 \\ 1&-2\end{array} \right)\)
\(\omega^2=\alpha\omega_0^2\) avec \(\alpha>0\)
\(\textrm{d\'et}(U+\omega^2I)=\textrm{d\'et} \omega_0^2\bigg[\left(\begin{array}{cc} -1&1 \\ 1&-2 \end{array} \right)+\left(\begin{array}{cc} \alpha&0 \\ 0&\alpha \end{array} \right)\bigg]=0\)
\(\Leftrightarrow\alpha=\frac{3\pm\sqrt5}{2}\Rightarrow \left|\begin{array}{l} \omega_1^2=\frac{3-\sqrt5}{2}\omega_0^2 \\ \omega_2^2=\frac{3+\sqrt5}{2}\omega_0^2 \end{array}\right. \Rightarrow\) mêmes pulsations propres que dans le système 2 masses 2 ressorts
\(\Rightarrow\) Matrice \(U_d\)
\(U_d=\omega_0^2\left(\begin{array}{cc} -\frac{3-\sqrt5}{2}&0 \\ 0& -\frac{3+\sqrt5}{2} \end{array}\right)\) telle que \(\left(\begin{array}{c} {\phi^1}'' \\ {\phi^2}'' \end{array} \right)=U_d\left(\begin{array}{c} \phi^1 \\ \phi^2 \end{array} \right)\)
\(\begin{array}{l}\phi^1=A^1\cos(\omega_1t+\alpha_1) \\ \phi^2=A^2\cos(\omega_2t+\alpha_2) \end{array}\) modes propres \(\phi^1=\left(\begin{array}{c} \phi^1 \\ 0\end{array} \right)\) et \(\phi^2=\left(\begin{array}{c} 0 \\ \phi^2 \end{array} \right)\)
Vecteurs propres \(M_1\) et \(M_2\) déterminés par \(UM_i=-\omega_i^2M_i\)
\(UM_i=\omega_0^2\left(\begin{array}{cc} -1&1 \\ 1&-2 \end{array} \right) \left(\begin{array}{c} 1 \\M_1^2 \end{array} \right) =\omega_0^2 \left(\begin{array}{cc} -1+M_1^2 \\ 1-2M_1^2 \end{array} \right) =-\omega_0^2\frac{3-\sqrt5}{2} \left(\begin{array}{c} 1 \\ M_1^2\end{array} \right)\)
\(\Rightarrow \left(\begin{array}{c} -\frac{3-\sqrt5}{2}=-1+M_1^2 \\ 1-2M_1^2=-\frac{3-\sqrt5}{2} M_1^2\end{array} \right) \Rightarrow M_1^2=\frac{-1+\sqrt5}{2}\) et \(M_1=\left(\begin{array}{c} 1 \\ M_1^2 \end{array} \right)\)
\(UM_2=\omega_0^2\left(\begin{array}{cc} -1&1 \\ 1&-2 \end{array} \right) \left(\begin{array}{c} 1 \\ M_2^2 \end{array} \right) =\omega_0^2\left(\begin{array}{c}\frac{-3-\sqrt5}{2}\\\frac{-3+\sqrt5}{2}M_2^2 \end{array} \right) \Rightarrow M_2^2=\frac{-1-\sqrt5}{2}\)
et \(M_2=\left(\begin{array}{c} 1 \\ M_2^2\end{array} \right)\)
\(\psi=M_1\phi^1+M_2\phi^2=\left(\begin{array}{c} 1 \\ \frac{-1+\sqrt5}{2} \end{array} \right) A^1\cos(\omega_1t+\alpha_1)+\left(\begin{array}{c} 1 \\ \frac{-1-\sqrt5}{2} \end{array} \right) A^2\cos(\omega_2t+\alpha_2)\)