Pendules couplés à ressort
Partie
Question
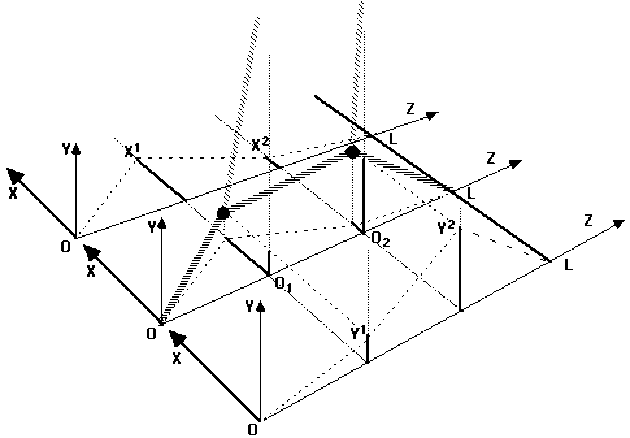
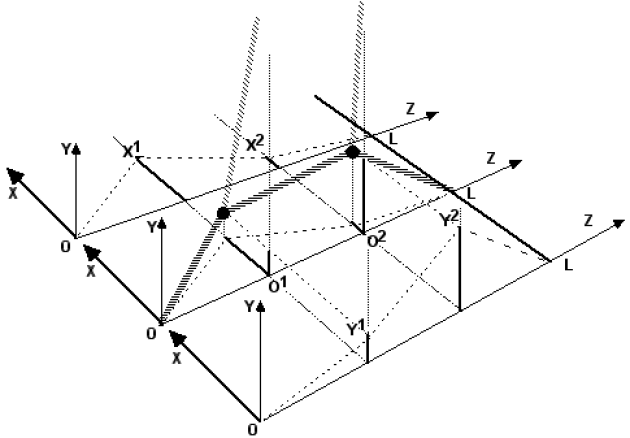
On considère le système constitué de 2 masses \(m^1\) et \(m^2\) identiques et égales à \(m\), suspendues par 2 ressorts identiques et de dureté \(K\).
Ces masses sont reliées entre elles et aux extrémités fixes \(O\) et \(L\) par des ressorts identiques (voir schéma ci-dessous). Les ressorts ont tous une masse négligeable.
Lorsque le système est au repos, les ressorts de suspension sont verticaux et les ressorts de couplages sont horizontaux et dirigés selon \(OZ\). La tension des ressorts de couplage est alors égale à \(T\).
Chacune des masses a un mouvement uniquement transversal. L'état du système sera donc déterminé par les paramètres \(X^1, Y^1, X^2, Y^2\) (coordonnées respectives des masses \(m^1\) et\( m^2\)).
Dans tout le problème, on ne considère que le cas des petites oscillations :
les variations angulaires de direction de tous les ressorts restent petites, ce qui autorise à confondre ces angles avec leur sinus ou tangente,
la longueur des ressorts de couplage reste approximativement constante et égale à : \(a = \frac{L}{3}\)
on suppose de plus que les ressorts de suspension ont une longueur très supérieure à celle ressorts de suspension n'intervient que dans la composante verticale des vibrations et pas dans la composante horizontale.
Autrement dit, pour chacune des masses (\(m^1\) resp. \(m^2\)) on considère donc que :
dans la composante de vibration selon \(OX\) seules interviennent les projections sur \(OX\) des forces de tension \(T\) des ressorts de couplage,
dans la composante de vibration selon \(OY\) on doit ajouter aux composantes verticales des tensions \(T\), la force de tension (\(t^1\) resp. \(t^2\)) du ressort vertical de suspension consécutive à sa variation de longueur (\(Y^1\) resp. \(Y^2\)) par rapport à sa position de repos (\(O^1\) resp. \(O^2\)).
Cette analyse du système et les approximations faites permettent de découpler les vibrations selon \(OX\) et \(OY\) et de les étudier séparément.
A- Composantes horizontales des vibrations.
A-1- Compte tenu de l'hypothèse exprimer les équations du mouvement horizontal pour chacune des masses, en déduire la matrice \(U\) correspondante : \(\ddot X=UX\)
A-2- Calculer ses valeurs propres en fonction de \(\omega_0^2=\frac{T}{ma}\)
A-3- En déduire ses vecteurs propres. Exprimer la vibration horizontale la plus générale.
B- Composantes verticales du mouvement.
B-1- Compte tenu de l'hypothèse exprimer les équations du mouvement vertical pour chacune des masses, en déduire la matrice \(V\) correspondante : \(\ddot Y=VY\)
B-2- Exprimer ensuite cette matrice dans le cas particulier où il existe la relation suivante entre les constante du système : \(K = \frac{2T}{a}\)
B-3- Calculer dans ce cas les pulsations propres.
B-4- En déduire les vecteurs propres de \(V\). Exprimer la vibration verticale la plus générale.
C- Mouvement général.
C-1- En notant \(\psi\) le vecteur d'état (de dimension 4) décrivant la vibration de ce système, déduire de ce qui précède l'expression de la matrice du système.
C-2- Exprimer la vibration générale sur la base des modes propres déterminés précédemment.
C-3- Déterminer la vibration du système dans le cas où il est lâché sans vitesse initiale et avec les positions initiales suivantes : \(X^1=0,~ Y^1=0,~ X^2=\frac{a}{20},~ Y^2=\frac{a}{10}\).
D- Relation entre composantes horizontales et verticales.
D-1- Exprimer la matrice \(V\) établie en -A.1- sous la forme \(V = U+A.I\) où I est la matrice unité de dimension 2 et où \(A\) est une constante que l'on explicitera.
D-2- En déduire la relation entre les valeurs propres des vibrations selon \(OX\) et \(OY\).
Rappel de cours
Voir la page Mise en équations
Solution détaillée
Remarquer l'égalité des composantes :
\(T_{1x}\equiv h_{1x}\)
\(T_{1y}\equiv V_{1y}\)
(idem pour les autres)
Mouvement Transversal dans les plans || XOY passant respectivement par \(O_1\) et \(O_2\)
(position de repos)
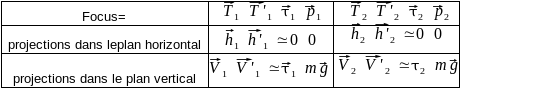
Approximation des petites oscillations :
(\(\cos \alpha \simeq1+O(\alpha^2)\)) (au second ordre près) idem pour les angles \(\theta\) et \(\varepsilon\)
\(Om_1\cos\varepsilon_1=OM_1 \Rightarrow om_1\simeq OM_1\simeq oo_1=a\) (idem pour les autres ressorts)
\(OO_1=OM_1\cos\alpha_1\)
A- Composantes horizontales du mouvement de \(m_1\) et \(m_2\)
\(||h_1||=||T_1||\cos\varepsilon_1\simeq ||T_1||\) et \(\sin\alpha_1=\frac{X^1}{a}\)
\(\Rightarrow h_{1x}=-||h_1||\sin\alpha_1\simeq-||T_1||\frac{X^1}{a}\) et de même :
\(h'_{1x}=||h'_{1x}||\sin\alpha'_1\simeq||T_1||\frac{X^2-X^1}{a}\)
attention aux signes , \(X^1>0\Rightarrow h_{1x}<0\) et \(X^2<X^1\Rightarrow h'_{1x}<0\)
Dans la suite : \(||T_1||=||T'_1||=||T_2||=||T'_2||=T\)
A-1
\(h_{1x}=-\frac{T}{a}x^1 h'_{1x}=\frac{T}{a}(X^2-X^2)\)
et de même : \(h'_{2x}=-h'_{1x}=\frac{T}{a}(x^1-x^2)h_{2x}=-\frac{T}{a}X^2\)
\(\sum\overrightarrow F=m\overrightarrow j\) en projection sur la direction X donne donc :
\(\left(\begin{array}{l} m\ddot X^1=\frac{T}{a}(-2X^1+X^2) \\ m\ddot X^2=\frac{T}{a}(X^1-2X^2) \end{array} \right) \Rightarrow \left(\begin{array}{c} \ddot X^1 \\ \ddot X^2 \end{array} \right)=\frac{T}{ma}\left(\begin{array}{cc} -2&1 \\ 1&-2 \end{array} \right)\left(\begin{array}{c} X^1 \\ X^2 \end{array} \right)\)
A-2
Calcul des valeurs propres par : \(\textrm{d\'et}(U + \omega^2 \pi) = 0\)
\(\left(\begin{array}{l} \frac{T}{a}=\omega_0^2 \\ \omega=\Omega\omega_0 \end{array} \right) \Rightarrow \textrm{d\'et}\left(\begin{array}{cc}-2+\Omega^2&1 \\ 1&-2+\Omega^2\end{array}\right)=0\)
\(\Leftrightarrow (-2+\Omega^2)^2-1=0 \Leftrightarrow (-2+\Omega^2-1)(-2+\Omega^2+1)=0\)
\(\Leftrightarrow (\Omega^2-3)(\Omega^2-1)=0\)
\(\omega_1=\omega_0 \qquad \Omega_1^2=1 \qquad \Omega_1=1\)
\(\omega_2=\sqrt3\omega_0\qquad \Omega_2^2=3 \qquad \Omega_2=\sqrt3\)
A-3
Vecteurs propres : \((U+\omega_i^2\pi)M_i=0\)
N°1 : \(M_1\) : \(\omega_0^2 \left(\begin{array}{cc}-2+1 & 1\\ 1 &-2+1\end{array}\right)\left(\begin{array}{c}1 \\ a\end{array}\right)=0 \left(\begin{array}{c} - 1+a=0 \\ 1-a=0\end{array}\right)\Rightarrow a=1\)
N°2 : \(M_1\) : \(\omega_0^2 \left(\begin{array}{cc}-2+3 & 1 \\ 1&-2+3\end{array}\right)\left(\begin{array}{c}1 \\ b\end{array}\right)=0 \left(\begin{array}{l}1+b=0 \\ 1-b=0\end{array}\right)\Rightarrow b=-1\)
\(M_1 : \left(\begin{array}{c}1\\ 1\end{array}\right) \qquad M_2 : \left(\begin{array}{c}1 \\ -1\end{array}\right)\)
Vibration générale horizontale :
\(X=\left(\begin{array}{c}X^1\\ X^2\end{array}\right) =A^1M_2\cos(\omega_1t+\varphi_1)+A^2M_2\cos(\omega_2t+\varphi_2)\)
B- Composantes verticales du mouvement.
B-1
Pour ce qui concerne les composantes verticales des Tensions des ressorts longitudinaux, on obtient les équations en remplaçant \(x\) par \(y\)
\(V_{1y}=-\frac{T}{a}y^1 \qquad V'_{1y}=\frac{T}{a}(y^2-y^1)\)
et \(V'_{2y}=-V'_{1y}=\frac{T}{a}(y^1-y^2) \qquad V_{2x}=-\frac{T}{a}y^2\)
Ressorts verticaux :
repos : \(\overrightarrow{\tau_{01}}+\overrightarrow{p_1}\)
mouvement : \(m_1\) écarté de \(y^1\Rightarrow\) variation de la tension \(\overrightarrow{t_1} : t_1=-Ky^1\)
\(\overrightarrow{\tau_1}=\overrightarrow{\tau_{01}}+\overrightarrow{t_1}y^1>0\Rightarrow t_1<0\)
(compression)
\(\overrightarrow{\tau_1}+\overrightarrow{p_1}=\overrightarrow{\tau_{01}}+\overrightarrow{t_1}+\overrightarrow{p_1}=\overrightarrow{t_1}\)
Equations du mouvement vertical
\(\left(\begin{array}{l} m\ddot y^1=\frac{T}{a}(-2y^1+y^2)-Ky^1 \\ m\ddot y^2=\frac{T}{a}(y^1-2y^2)-Ky^2 \end{array} \right) \Rightarrow \left(\begin{array}{c} \ddot y^1 \\ \ddot y^2 \end{array} \right)=\left(\begin{array}{c} \frac{T}{ma}(-2y^1+y^2) -\frac{K}{m}y^1\\ \frac{T}{ma}(y^1-2y^2) -\frac{K}{m}y^2\end{array} \right)\)
B-2
En remplaçant : \(K=2\frac{T}{a}\Rightarrow \left(\begin{array}{c}\ddot y^1 \\ \ddot y^2 \end{array}\right)=\frac{T}{ma}\left(\begin{array}{c}-4y^1+y^2\\ y^1-4y^2 \end{array}\right)\)
B-3
\(\ddot y=\left(\begin{array}{c}\ddot y^1 \\ \ddot y^2 \end{array}\right)=\omega_0^2\left(\begin{array}{cc}-4&1 \\1&-4 \end{array}\right)\left(\begin{array}{c} y^1\\ y^2 \end{array}\right)\) posons \(\omega=\omega_0\)
\(\textrm{d\'et}(U+\omega_0^2 \pi)=\omega_0^2\textrm{d\'et}\left(\begin{array}{cc} -4+\Omega^2&1\\ 1&-4+\Omega^2 \end{array}\right)=0\)
\(\Rightarrow (-4+\Omega^2)-1=(-4+\Omega^2-1)(-4+\Omega^2+1)=(-5+\Omega^2)(-3+\Omega^2)\)
\(\Rightarrow \left|\begin{array}{l} \Omega_1^2=3 \\ \Omega_2^2=5 \end{array} \right. \qquad\qquad \Rightarrow \left|\begin{array}{l} \omega_3=\sqrt3 \omega_0 \\ \omega_4=\sqrt5\omega_0\end{array}\right.\)
les vecteurs propres \(\overrightarrow{M_3}\) et \(\overrightarrow{M_4}\) sont déterminés par la méthode générale (ou bien question 4)
Méthode générale : \((U+\omega_i^2\pi)M_i=0\)
vecteur propre n°3 : \(\omega_0^2\left(\begin{array}{cc} -4+3&1 \\ 1&-4+3\end{array} \right)\left(\begin{array}{c} 1 \\ a\end{array} \right)=0\)
\(\left(\begin{array}{cc} -1&1 \\1&-1\end{array} \right)\left(\begin{array}{c} 1 \\ a\end{array} \right)\left(\begin{array}{cc} -1+a \\ 1-a\end{array} \right)=\left(\begin{array}{c} 0 \\ 0\end{array} \right) \Leftrightarrow a=1\Rightarrow M_3=\left(\begin{array}{c} 1\\ 1\end{array}\right)\)
vecteur propre n°4 :
\(\omega_0^2\left(\begin{array}{cc} -4+5 & 1 \\ 1&-4+5\end{array} \right)\left(\begin{array}{c} 1 \\ b\end{array} \right)=0\)
\(\left(\begin{array}{cc} 1&1 \\1&1\end{array} \right)\left(\begin{array}{c} 1 \\ b\end{array} \right)\left(\begin{array}{cc} -1+b\\ 1-b\end{array} \right)=\left(\begin{array}{c} 0 \\ 0\end{array} \right) \Leftrightarrow b=1\Rightarrow M_4=\left(\begin{array}{c} 1\\ -1\end{array}\right)\)
(mêmes vecteurs propres que pour le mouvement horizontal).
\(y=\left(\begin{array}{c}y^1 \\y^2\end{array} \right)=A^3M_3\cos(\omega_3t+\varphi_3)+A^4M_4\cos(\omega_4t+\varphi_4)\)
avec \(M_3=\left(\begin{array}{c} 1 \\1\end{array} \right)=M_1 \qquad M_4=\left(\begin{array}{c} 1 \\-1\end{array} \right)=M_2\)
\(\omega_3=\sqrt3\omega_0=\omega_2 \qquad \omega_4=\sqrt5\omega_0\)
C- Mouvement général
C-1
\(\ddot{\psi}=\left(\begin{array}{c} \ddot X^1 \\ \ddot X^2 \\ \ddot X^3 \\ \ddot X^4 \end{array} \right)=\omega_0^2 \left(\begin{array}{cccc}-2&1&0&0\\ 1&-2&0&0 \\ 0&0&-4&1\\ 0&0&1&-4 \end{array} \right)\left(\begin{array}{c} X^1 \\ X^2 \\ X^3 \\ X^4 \end{array} \right)\)
car \(\ddot{\psi}=\left(\begin{array}{c} \ddot X\\ \ddot Y \end{array} \right)=\left(\begin{array}{cc} U&0\\ 0&V \end{array} \right)\left(\begin{array}{c} X\\ Y \end{array} \right)=\left(\begin{array}{cc} U&X \\ V&Y \end{array} \right)\)
C-2
Vibration générale \(\psi=\left(\begin{array}{cc} X\\ Y \end{array} \right)=\left(\begin{array}{cc} X^1 \\ X^2 \\ Y^1 \\ Y^2\end{array} \right)\)
\(\psi=\left(\begin{array}{c} A^1M_1\cos(\omega_1t+\varphi_1)+A^2M_2\cos(\omega_2t+\varphi_2)\\A^3M_3\cos(\omega_3t+\varphi_3)+ A^4M_4\cos(\omega_4t+\varphi_4) \end{array} \right)\)
dans l'espace de dimension 4, les modes propres doivent avoir 4 composantes :
\(M_1=\left(\begin{array}{c} M_1 \\0\\0\end{array}\right)=\left(\begin{array}{c} 1\\1\\0\\0\end{array}\right) \qquad\qquad M_2=\left(\begin{array}{c} M_2 \\0\\0\end{array}\right)=\left(\begin{array}{c} 1\\-1\\0\\0\end{array}\right)\)
\(M_3=\left(\begin{array}{c} 0 \\0\\M_3\end{array}\right)=\left(\begin{array}{c} 0\\0\\1\\1\end{array}\right)\qquad\qquad M_4=\left(\begin{array}{c} 0 \\0\\M_4\end{array}\right)=\left(\begin{array}{c} 0\\0\\1\\-1\end{array}\right)\)
alors : \(\psi=\displaystyle{\sum_{i=1}^4A^iM_i\cos(\omega_it+\varphi_i)}\)
C-3
Conditions initiales vitesse initiale\(=0\Leftarrow \varphi_i=0\)
\(\Rightarrow \psi_{t=0}=\displaystyle{\sum_iA^iM_i}=\left(\begin{array}{c} 0 \\ \frac{a}{20} \\ 0 \\\frac{a}{10}\end{array}\right)\)
\(\Rightarrow \left(\begin{array}{c} A^1+A^2=0\\A^1-A^2=\frac{a}{20}\\A^3+A^4=0\\A^3-A^4=\frac{a}{10}\end{array}\right)\Rightarrow \begin{array}{l} A^2=-A^1\Rightarrow 2A^1=\frac{a}{20}\Rightarrow A^1=\frac{a}{40} \\A^4=-A^3\Rightarrow 2A^3=\frac{a}{10}\Rightarrow A^3=\frac{a}{20}\end{array}\)
D- Relation entre composantes horizontales et verticales.
\(\frac{T}{ma}=\omega_0^2-\frac{K}{m}=A\)
\(\Rightarrow \ddot{\psi}=\left(\begin{array}{c} \ddot X^1 \\ \ddot Y^2 \end{array}\right)=[\omega_0^2 \left(\begin{array}{cc} -2&1 \\ 1&-2 \end{array}\right)+A\left(\begin{array}{cc} 1&0 \\ 0&1 \end{array}\right)]\left(\begin{array}{c} y^1 \\ y^2 \end{array}\right)=(U+A \pi)y\)
\(\ddot{\psi}=Vy\) soit \(V=U+A \pi\Rightarrow\) (\(\pi\) étant une diagonale \(\Rightarrow\) \(V\) a les mêmes vecteurs propres que \(U\))
\(V=U+A \pi\) avec \(A=-\frac{K}{m}\)
\(\textrm{d\'et}(V+\omega_v^2 \pi)=0\Leftrightarrow \textrm{d\'et}(U+A \pi+\omega_v^2 \pi)=0\) mais \(\textrm{d\'et}(U+\omega_v^2 \pi)=0\)
\(\Rightarrow\) solution \({\omega'}_v^2=A+\omega_v^2\)
\(\omega_v^2={\omega'}_v^2-A={\omega'}_v^2+\frac{K}{m}\)
retour à l'AN précedente : \(\frac{K}{m}=\frac{2T}{ma}\Rightarrow K=\frac{2T}{a}\)
\(\begin{array}{l}\omega_{v1}^2=\omega_0^2\Rightarrow \omega_{v1}^2=3\omega_0^2 \\ \omega_{v2}^2=3\omega_0^2 \Rightarrow \omega_{v2}^2=5\omega_0^2 \end{array} \Rightarrow \frac{K}{m}=2\omega_0^2\)