Système 6 condensateurs - 5 selfs
Partie
Question
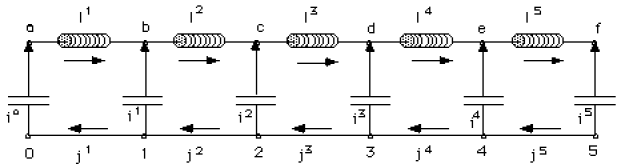
Dans ce système, les Selfs ont toutes la même valeur \(L\) et les Condensateurs ont tous la même capacité \(C\) . On posera : \(\omega_0^2=\frac{1}{LC}\) Certaines relations peuvent s'obtenir par permutations d'exposants : il est pour cela nécessaire de respecter les notations de la figure ainsi que les sens positifs indiqués par les flèches.
Exprimer la dérivée seconde de \(I^1\) en fonction de \(\omega_0^2\), \(i^0\) et \(i^1\).
Exprimer ensuite les 4 relations analogues concernant les courants \(I^2\), \(I^3\), \(I^4\) et \(I^5\)
Indiquer les relations : entre \(i^0\) et \(I^1\), et entre \(i^5\) et \(I^5\).
Indiquer les relations entre les courants aux nœuds : \(b\), \(c\), \(d\) et \(e\).
En utilisant les 5 relations trouvées question -1-, en déduire les 5 équations différentielles reliant les courants \(I^n\) \((1\le n \le5)\). Mettre ce système d'équations couplées sous forme matricielle.
On notera \(\psi\) le vecteur de composantes \(I^n\) \((1\le n\le5)\) et \(U\) la matrice correspondante.
Déterminer les pulsations propres \(\omega_p\) du système.
(Ces pulsations seront notées : \((\omega_p)^{2} = \alpha_p . ( \omega_0)^2\) (avec \(\alpha_p > 0\)) et numérotées par ordre de valeurs croissantes). En déduire la matrice \(U_d\) qui est diagonale dans le système de coordonnées notées \((\phi)\), ainsi que la forme des solutions \(\phi^p\).
Déterminer le second vecteur propre \(M_2\) de la matrice \(U\), ainsi que l'expression du mode propre \(\psi_2\) correspondant. (Les composantes des vecteurs propres \(M_p\) seront notées : \(M_p^n\)).
Déterminer les autres vecteurs propres \(M_p\) de la matrice \(U\) à partir de l'expression générale : \(M_p^n=\sin[\frac{np\pi}{(N+1)}]\) relative à un système de dimension \(N\).
En déduire l'expression générale des courants dans ce système.
Représenter un système mécanique régi par le même système différentielles.
En préciser les variables.
Rappel de cours
Voir la page Mise en équations
Solution détaillée
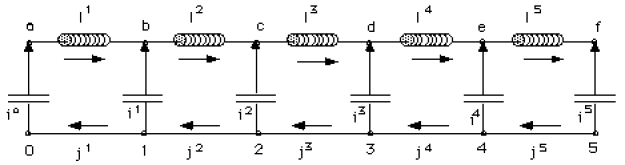
Notations :
les variables qui définissent l'état du système (courants et tensions) sont notées, comme dans le cours, avec un exposant.
Rappel :
Pour une self : \(e=-L\frac{di}{dt}=V_{\textrm{sortie}}-V_{\textrm{entr\'ee}}\)
Pour un condensateur : \(V_{\textrm{sortie}}-V_{\textrm{entr\'ee}}=\frac{q_{\textrm{sortie}}}{C}\)
\(i=-\frac{dq_s}{dt}\) avec la convention des sens : \(\parallel q_s \to +\)
Ce qu'on appelle entrée ou sortie d'un élément est défini par le sens de parcours choisi pour la maille.
\(\left.\begin{array}{l} V_b-V_a=-L\frac{dI^1}{dt} \\ V_a-V_0=\frac{q^0}{C} \end{array} \right| \Rightarrow V_b-V_0=-L\frac{dI^1}{dt}+\frac{q^0}{C}\)
\(V_b-V_0=V_b-V_1=\frac{q^1}{C}\Rightarrow L\frac{dI^1}{dt}+\frac{q^0}{C}=\frac{q^1}{C}\) \(\Rightarrow \frac{dI^1}{dt}=\frac{1}{LC}(q^0-q^1)\)
Les autres équations peuvent être obtenues par permutations d'exposants : \(\Rightarrow \begin{array}{l} \frac{d^2I^1}{dt^2}=\omega_0^2(-i^0+i^1) \\ \frac{d^2I^2}{dt^2}=\omega_0^2(-i^1+i^2) \\\frac{d^2I^3}{dt^2}=\omega_0^2(-i^2+i^3) \\ \frac{d^2I^4}{dt^2}=\omega_0^2(-i^3+i^4) \\ \frac{d^2I^5}{dt^2}=\omega_0^2(-i^4+i^5) \end{array}\)
Relations entre courants :
\(i^0=I^1 \qquad I^2=i^1+I^1 \qquad I^3=i^2+I^2 \qquad I^4=i^3+I^3 \qquad I^5=i^4+I^4 \qquad i^5=-I^5\)
Equations différentielles :
\(-i^0+i^1=-I^1+(-I^1+I^2) \quad \Rightarrow (I^1)''=\omega_0^2(-2I^1+I^2)\)
\(-i^1+i^2=(I^1-I^2)+(-I^2+I^3) \Rightarrow (I^2)''=\omega_0^2(I^1-2I^2+I^3)\)
\(-i^2+i^3=(I^2-I^3)+(-I^3+I^4) \Rightarrow (I^3)''=\omega_0^2(I^2-2I^3+I^4)\)
\(-i^3+i^4=(I^3-I^4)+(-I^4+I^5) \Rightarrow (I^4)''=\omega_0^2(I^3-2I^4+I^5)\)
\(-i^4+i^5=(I^4-I^5)+(-I^5) \quad \Rightarrow (I^5)''=\omega_0^2(I^4-2I^5)\)
En posant : \(\psi=\left(\begin{array}{c} I^1 \\ I^2 \\I^3 \\I^4 \\I^5 \end{array}\right) \Rightarrow\) le système précédent s'écrit sous la forme \(\psi''=U\psi\)
On obtient la même matrice \(U\) que dans le système 5 masses : \(U=\omega_0^2\left(\begin{array}{ccccc} -2&1&0&0&0 \\ 1&-2&1&0&0 \\ 0&1&-2&1&0 \\ 0&0&1&-2&1 \\ 0&0&0&1&-2\end{array}\right)\)
On pose \(\omega^2=a\omega_0^2\) et on résoud ; \(\textrm{d\'et}(U+\omega^2 \pi)=0\)
\(u_5=\left(\begin{array}{ccccc} -2+\alpha&1&0&0&0 \\ 1&-2+\alpha&1&0&0 \\ 0&1&-2+\alpha&1&0 \\ 0&0&1&-2+\alpha&1 \\ 0&0&0&1&-2+\alpha\end{array}\right)=\left(\begin{array}{ccccc} a&1&0&0&0 \\ 1&a&1&0&0 \\ 0&1&a&1&0 \\ 0&0&1&a&1 \\ 0&0&0&1&a\end{array}\right)\)
(en posant \(a=-2+\alpha\) pour simplifier l'écriture)\(\Rightarrow\) \(\textrm{d\'et}(u_N)=a ~\textrm{d\'et}(u_{N-1})-\textrm{d\'et}(u_{N-2})\) pour \(N>2\)
\(\textrm{d\'et}(u_3)=a ~ \textrm{d\'et}(u_4)-\textrm{d\'et}(u_3)\)
\(\textrm{d\'et}(u_4)=a ~ \textrm{d\'et}(u_3)-\textrm{d\'et}(u_2)\) et \(\textrm{d\'et}(u_2)=a^2-1\)
\(\textrm{d\'et}(u_5)=a ~ \textrm{d\'et}(u_2)-\textrm{d\'et}(u_1)\) et \(\textrm{d\'et}(u_1)=a\)
\(\Rightarrow \textrm{d\'et}(u_3)=a(a^2-1)-a=a(a^2-2)\)
\(\Rightarrow \textrm{d\'et}(u_4)=a[a(a^2-2)]-[(a^2-1)]\)
\(\Rightarrow \textrm{d\'et}(u_5)=a^2[a(a^2-2)]-a[a^2-1]-a(a^2-2)=a(a^2-2)(a^2-1)-a(a^2-1)=a(a^2-1)[(a^2-2)-1]\)
\(\textrm{d\'et}(u_5)=a(a^2-1)(a^2-3)\)
\(\textrm{d\'et}(U+\omega^2 \pi)=0 \Leftrightarrow \textrm{d\'et}(u_5)=0~(\textrm{avec } a = +2 +a )\Leftrightarrow \left\{\begin{array}{r} a=0 ~(1)\\ a^2-1=0 ~(2) \\ a^2-3=0 ~(3) \end{array}\right.\)
Solutions :
\(\textrm{N}^{\circ} \textrm{par ordre}\)
\(\textrm{croissant}\)
\((1)\)
\(\Leftrightarrow\)
\(\alpha = 2\)
\(\qquad\) \(\qquad\) \(~3\)
\(\omega_1=\sqrt{2-\sqrt3}~\omega_0\)
\((2)\)
\(\Leftrightarrow\)
\(a = 1\)
\(\Leftrightarrow\)
\(\alpha = 3\)
\(\qquad\) \(\qquad\) \(~4\)
\(\omega_2=\omega_0\)
\(\alpha = 1\)
\(\qquad\) \(\qquad\) \(~2\)
\(\Rightarrow\)
\(\omega_3=\sqrt2~\omega_0\)
\(\alpha = 2 + \sqrt{3}\)
\(\qquad\) \(\qquad\) \(~5\)
\(\omega_4=\sqrt3~\omega_0\)
\(\alpha = 2 - \sqrt{3}\)
\(\qquad\) \(\qquad\) \(~1\)
\(\omega_5=\sqrt{2+\sqrt3}~\omega_0\)
Le résultat général (ordre \(N\)) est \(\omega_p=2\omega_0\sin\frac{p\pi}{2(N+1)}\)
En faisant \(N=5\), on retrouve bien ces valeurs.
On a alors : \(\ddot{\phi}=U_d\phi\) avec \(U_d=\left(\begin{array}{ccccc} -\omega_1^2&0&0&0&0 \\ 0& -\omega_2^2&0&0&0 \\ 0&0&-\omega_3^2&0&0 \\ 0&0&0&-\omega_4^2&0 \\ 0&0&0&0&-\omega_5^2\end{array} \right)\)
et \(\phi=\left(\begin{array}{c} \phi^1 \\ \phi^2 \\ \phi^3 \\ \phi^4 \\ \phi^5 \end{array}\right)\) avec \(\phi^p=A^p\cos(\omega_pt+\varphi_p)\)
Le mode propre de rang \(p\) en coordonnées \((\phi)\) est \(\phi_p=\left(\begin{array}{c} 0 \\ 0 \\ \phi^p \\ 0\\ 0 \end{array}\right)\)
Les directions propres \(M_i\) de \(U\) sont déterminés par (\(UM_i=-\omega_i^2M_i\))
\(\Rightarrow\) direction propre \(M_2\Rightarrow(U+\omega_i^2 \pi)M_2=0\)
On pose \(M_2^1=1\) (arbitrairement, puisque tous les coefficients ne sont déterminées qu'à un facteur multiplicatif près).
\(\left(\begin{array}{ccccc} -1&1&0&0&0 \\ 1&-1&1&0&0 \\ 0&1&-1&0&0 \\ 0&0&1&-1&1 \\ 0&0&0&1&1\end{array} \right) \left(\begin{array}{c} 1\\ M_2^2 \\ M_2^3 \\ M_2^4 \\ M_2^5\end{array} \right)=0\begin{array}{l}\Rightarrow -1+M_2^1=0 \\ \Rightarrow 1-1+M_2^3=0\\ \Rightarrow 1+0+M_2^4=0 \\ \Rightarrow 0+1+M_2^5=0 \\ \Rightarrow -1+1=0 \end{array}\Rightarrow \begin{array}{l} M_2^1=1 \\ M_2^2=1 \\M_2^3=0 \\ M_2^4=-1 \\ M_2^5=-1 \end{array}\)
Expressions générale des vecteurs propres :
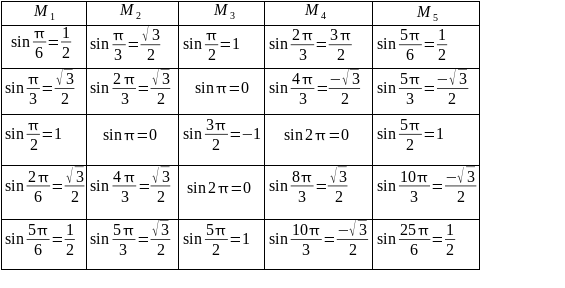
Notation : \(M_{p \gets \textrm{N}^{\circ}\textrm{de mode propre}}^{n \gets \textrm{N}^{\circ} \textrm{de la ligne de }M_p}\Rightarrow M_p=\left(\begin{array}{c} \sin(p\frac{\pi}{6})\\ \sin(2p\frac{\pi}{6}) \\\sin(3p\frac{\pi}{6}) \\\sin(4p\frac{\pi}{6})\\ \sin(5p\frac{\pi}{6})\end{array} \right)\)
7. Vibration générale
\(\psi=\psi_1-\psi_2+\psi_3+\psi_4+\psi_5\)
Les modes propres \(\psi_p\) sont définis par : \(\psi_p=M_p \phi^p\)
avec \(\phi^p=A^p\cos(\omega_pt+\varphi_p)\)
\(\psi=\left(\begin{array}{c} I^1 \\I^2\\I^3\\I^4\\I^5\end{array}\right)\)
Analogue mécanique : vibrations d'un système 5 masses - 6 ressorts (voir exercice)
avec \(\psi=\left(\begin{array}{c} x^1 \\x^2\\x^3\\x^4\\x^5\end{array}\right)\) où \(x^i\) représente la coordonnée de la masse N°i par rapport à sa position de repos.