Système 3 masses - 4 ressorts
Partie
Question
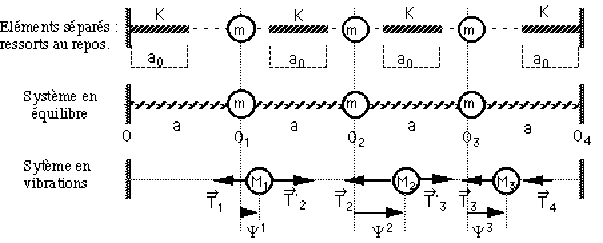
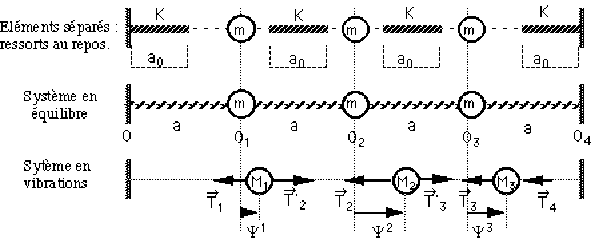
On considère le système constitué de 3 masses identiques, reliées par des ressorts identiques, et assujetties à se déplacer sur un même axe horizontal \(\psi\), sans frottement.
Mise en équation.
Appliquer à chacune des masses le principe fondamental de la dynamique.
Indiquer le nombre de variables indépendantes utilisées pour décrire l'état vibratoire de ce système et son nombre de degrés de liberté. Ecrire les équations du mouvement avec les variables \(\psi^1, \psi^2, \psi^3\).
La résolution du système d'équations obtenues est-elle possible :
directement, comme dans le cas du pendule sphérique ?
par un changement de variables simple, comme dans le cas du système 2 masses, 3 ressorts ?
Rappel sur la méthode générale de traitement.
La méthode concernant un système à 2 degrés de liberté, se généralise à l'ordre 3 :
L'état \(\psi\) : \(\left(\begin{array}{l} \psi^1 \\ \psi^2 \\ \psi^3 \end{array} \right)\) du système satisfait la relation : \(\ddot{\psi}=U\psi\)
On doit rechercher le changement de variables : \(\psi = M. \phi\), tel que la matrice représentant le système dans ces coordonnées \(\phi\) soit alors une matrice \(U_d\) diagonale
soit : \(\ddot{\phi}=U_d\phi\) avec \(U_d : \left(\begin{array}{ccc} -\omega_1^2&0&0 \\ 0&-\omega_2^2&0 \\ 0&0&-\omega_3^2 \end{array} \right)\)
On pose la matrice \(M\) sous la forme : \(M=[M_1, M_2, M_3]\) ,
d'où : \(U.M =U[M_1, M_2, M_3]\)
Montrer qu'alors : \(\begin{array}{l} U.M_1=-\omega_1^2.M_1 \\ U.M_2=-\omega_2^2.M_2 \\ U.M_3=-\omega_3^2.M_3 \end{array}\)
On détermine donc les pulsations propres \(\omega\) du système par la résolution de :
\(\textrm{d\'et}[U+\omega_2I]=0\) (où \(I\) désigne la matrice unité).
Résolution
Ecrire et résoudre l'équation aux pulsations propres.
Résoudre le système \(\ddot{\phi}=U_d.\phi\)
Ecrire les modes propres : \(\phi_1, \phi_2, \phi_3\).
Déterminer la matrice \(M=[M_1, M_2, M_3]\)
En déduire les modes propres :
\(\psi_1=\left(\begin{array}{l} \psi^1 \\ \psi^2 \\ \psi^3 \end{array} \right)_1 \quad \psi_2=\left(\begin{array}{l} \psi^1 \\ \psi^2 \\ \psi^3 \end{array} \right)_2 \quad \psi_3=\left(\begin{array}{l} \psi^1 \\ \psi^2 \\ \psi^3 \end{array} \right)_3\)
Sur 3 schémas distincts, représenter la position des masses correspondant à la vibration du système selon chacun de ces modes propres.
On considère alors la vibration particulière correspondant aux conditions initiales suivantes :
\(t=0\Rightarrow \dot{\psi}^1=\dot{\psi}^2=\dot{\psi}^3=0\)
\(\psi^1=\psi^3=0\) et \(\psi^2=1\)
Vérifier alors que le vecteur : \(\psi = M\left(\begin{array}{l} A^1\cos\omega_1t \\ A^2\cos\omega_2t \\ A^3\cos\omega_3t \end{array} \right)\) satisfait les conditions initiales sur la vitesse.
Déterminer les amplitudes \(A^1, A^2, A^3\) de vibration de chacune des masses.
Exprimer les solutions : \(\psi^1, \psi^2, \psi^3\) sous forme de produits de fonctions sinus et cosinus. Décrire le phénomène de battements obtenus.
Aide simple
Exprimez les allongements algébriques par rapport aux positions de "repos".
On doit trouver une matrice U du système : \(U=\omega_0^2\left(\begin{array}{ccc} -2&1&0\\ 1&-2&1 \\ 0&1&-2 \end{array} \right)\)
Rappel de cours
Voir la page Résolution
Solution détaillée
1- Mise en équation.
Les 3 masses identiques, reliées par des ressorts identiques, sont assujetties à se déplacer sur le même axe horizontal \(\psi\), sans frottement \(\Rightarrow\) le poids et la réaction de l'axe \(\psi\) de guidage sont verticaux, donc orthogonaux au mouvement de chacune des masses.
Les seules forces intervenant sont donc les forces de tension des ressorts.
Chaque masse a 1 degré de liberté (mouvement sur l'axe \(\psi\)) et pour connaitre l'état du système, il est nécessaire de connaitre la position de chacune des masses. Le système a donc 3 degrés de liberté et son état sera représenté par le vecteur : \(\psi=\left|\begin{array}{c} \psi^1 \\ \psi^2 \\ \psi^3 \end{array} \right|\)
Longueur des 4 ressorts
\(l_1=\overline{OM_1}=\overline{OO_1}+\overline{O_1M_1}=a+\psi^1\)
\(l_2=\overline{M_1M_2}=\overline{M_1O_1}+\overline{O_1O_2}+\overline{O_2M_1}=-\psi^1+a+\psi^2\)
\(l_3=\overline{M_2M_2}=\overline{M_2O_2}+\overline{O_2O_3}+\overline{O_3M_3}=-\psi^2+a+\psi^3\)
\(l_4=\overline{M_3O_4}=\overline{M_3O_3}+\overline{O_3O_4}=-\psi^3+a\)
Allongements par rapport au "repos"
\(l_1-a_0=a-a_0+\psi^1\)
\(l_2-a_0=a-a_0-\psi^1+\psi^2\)
\(l_3-a_0=a-a_0-\psi^2+\psi^3\)
\(l_4-a_0=a-a_0-\psi^3\)
Chaque masse \(M_i\) i est soumise à 2 forces : \(\overrightarrow{T_i}\) et \(\overrightarrow{T_{i+1}}\) qui se projettent respectivement en \(T_i\) et \(T'_{i+1}\) sur l'axe \(\psi\). Ces projections sont évidemment algébriques :
\(T_i < 0\) si le ressort correspondant est étiré, et \(T_i > 0\) si le ressort correspondant est contracté
\(T'_{i+1} > 0\) si le ressort correspondant est étiré, et \(T'_{i+1 }< 0\) si le ressort correspondant est contracté.
Le PFD appliqué à la masse i donne : \(F_i=T_i+T'_{i+1}=m\ddot{\psi^i}\)
avec \(T_i=-K(l_i-a_0)\) et \(T'_{i+1}=+K(l_{i+1}-a_0)\)
ce qui donne (algébriquement) :
\(T_1=-K(l_1-a_0)=-K(a-a_0)-K\psi^1\)
\(T_2=-K(l_2-a_0) = -K.(a-a_0) +K(\psi^1-\psi^1)=-T'_{2}\)
\(T_3=-K(l_3-a_0) = -K.(a-a_0) +K(\psi^2-\psi^1)=-T'_{3}\)
\(T'_{4}=-K.(l_4-a_0)=+K(a-a_0)-K\psi^1\)
Sur la masse 1 : \(F_1=T_1+T'_{1}=-K\psi^1-K(\psi^1-\psi^2)=-2.K.\psi^1+K.\psi^2\)
Sur la masse 2 : \(F_2=T_2+T'_{3}=K(\psi^1-\psi^2)-K(\psi^2-\psi^3)=K\psi^1-2K\psi^2+K\psi^3\)
Sur la masse 3 : \(F_2=T_3+T'_{4}=K.(\psi^2-\psi^3)-K.\psi^3=K.\psi^2-2K.\psi^3\)
(les termes en \(K(a-a_0)\) s'annulent 2 à 2).
On pose \(\frac{K}{m}=\omega_0^2\Rightarrow\) Masse 1 : \(\ddot{\psi}^1=\omega_0^2.(-2\psi^1+\psi^2)\)
Masse 2 : \(\ddot{\psi}^2=\omega_0^2(\psi^1-2\psi^2+\psi^3)\)
Masse 3 : \(\ddot{\psi}^3=\omega_0^2.(\psi^2-2\psi^3)\)
2- Méthode
Ces 3 équations s'expriment sous forme matricielle : \(\ddot{\psi}=U.\psi\)
avec \(U=\omega_0^2 . \left(\begin{array}{ccc} -2&1&0\\ 1&-2&1 \\ 0&1&-2 \end{array} \right)\)
On applique la méthode générale :
\(U.M=U(M_1, M_2, M_3)=(UM_1, UM_2, UM_3)\)
\(MU_d=(M_1, M_2, M_3). \left(\begin{array}{ccc} -\omega_1^2&0&0\\ 0&-\omega_2^2&0 \\ 0&0& -\omega_3^2 \end{array} \right)=(-\omega_1^2M_1, -\omega_2^2M_2 , -\omega_3^2M_3)\)
\(U.M=M.U_d\Rightarrow U.M_1=-\omega_1^2 .M_1\). On pose : \(\omega_1=u_1 .\omega_0\)
\(U.M_2=-\omega_2^2 .M_2\omega_2=u_2 .\omega_0\)
\(U.M_3=-\omega_3^2 .M_3\omega_3=u_3 .\omega_0\)
3- Résolution
On résout ce système en écrivant :
\(\textrm{d\'et}(U+\omega^2I)=0\Rightarrow \left(\begin{array}{ccc} -2+u^2&1&0\\ 1&-2+u^2&1 \\ 0&1&-2+u^2 \end{array} \right)=0\)
\(\Rightarrow (-2+u^2)\left(\begin{array}{cc} -2+u^2&1\\ 1&-2+u^2 \end{array} \right)+\left(\begin{array}{cc} 1&1\\ -2+u^2&0 \end{array} \right)+0\)
\(\Rightarrow (-2+u^2)[(-2+u^2)^2-1]-(-2+u^2)=0\)
\(\Rightarrow(-2+u^2)[(-2+u^2)^2-2]=0\)
1° solution : \((-2+u^2)=0 \Rightarrow u^2=2\)
2° solution : \([(-2+u^2)^2-2]=0\Rightarrow -2+u^2=\sqrt2\)
\(\Rightarrow[(-2+u^2)-\sqrt2)][(-2+u^2)+\sqrt2]=0\) ou \(-2+u^2=-\sqrt2\)
Les pulsations propres sont finalement : \(\omega_1^2=(2-\sqrt2).\omega_0^2\)
\(\omega_2^2=2.\omega_0^2\)
\(\omega_3^2=(2+\sqrt2).\omega_0^2\)
Les pulsations propres \(\omega_i\) permettent d'exprimer les fonctions propres \(\phi^i\) solutions du système diagonal : \(\ddot{\phi}=U_d\phi\), soit :
\(\phi^1=A^1\cos(\omega_1t+\alpha_1)\)
\(\phi^2=A^2\cos(\omega_2t+\alpha_2)\)
\(\phi^3=A^3\cos(\omega_3t+\alpha_3)\)
Les modes propres en coordonnées \(\phi\) sont solution de l'équation \(\ddot{\phi}= U_d . \phi\), soit :
\(\phi_1=\left(\begin{array}{c} \phi^1 \\ 0\\0 \end{array}\right) \quad \phi_2=\left(\begin{array}{c} 0\\ \phi^2\\0 \end{array}\right) \quad \phi_3=\left(\begin{array}{c} 0 \\ 0\\\phi^3 \end{array}\right)\)
Pour déterminer les directions propres \(M_i\), on peut par exemple poser la 1° composante égale à 1.
Il faut ensuite reporter les valeurs \(\omega_i\) dans l'équation matricielle :
\(UM_i+\omega_i^2M_i=0 \Leftrightarrow \left(\begin{array}{ccc} -2+u_i^2&1&0\\ 1&-2+u_i^2&1 \\ 0&1&-2+u_i^2 \end{array} \right)\left(\begin{array}{c} 1\\ a_i\\b_i \end{array} \right)=0\)
(Voir, à la fin de ce corrigé, le détail de cette résolution).
On trouve à un coefficient multiplicatif près :
\(M_1=\left|\begin{array}{c}1 \\ \sqrt2 \\1 \end{array}\right| \quad M_2=\left|\begin{array}{c}1 \\ 0 \\-1 \end{array}\right| \quad M_3=\left|\begin{array}{c}1 \\ -\sqrt2 \\1 \end{array}\right|\)
et les modes propres de vibration en coordonnées \(\psi\) s'expriment :
\(\psi_1=\left|\begin{array}{c}1 \\ \sqrt2 \\1 \end{array}\right|\phi^1 \quad \psi_2 = \left|\begin{array}{c}1 \\ 0 \\-1 \end{array}\right|\phi^2 \quad \psi_3 = \left|\begin{array}{c}1 \\ -\sqrt2 \\1 \end{array}\right|\phi^3\)
\(M_1\), \(M_2\) et \(M_3\) déterminent (dans chacun des 3 modes propres) les rapports d'amplitudes des oscillations des masses. (schéma ci-après).
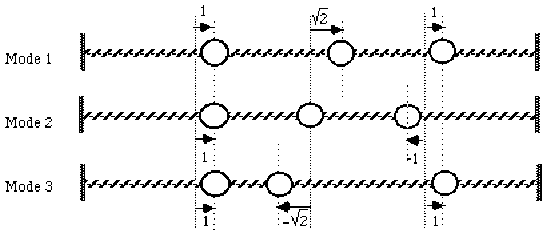
Vibration générale :
\(\psi=\psi_1+\psi_2+\psi_3=\left|\begin{array}{c}\psi^1\\ \psi^2 \\\psi^3 \end{array}\right|\)
\(\Rightarrow \psi=\psi_1+\psi_2+\psi_3=\left(\begin{array}{ccc} A^1\cos(\omega_1t+\alpha_1)&+A^2\cos(\omega_2t+\alpha_2)&+A^3\cos(\omega_3t+\alpha_3)\\ \sqrt2A^1\cos(\omega_1t+\alpha_1)&0&-\sqrt2A^3\cos(\omega_3t+\alpha_3) \\ A^1\cos(\omega_1t+\alpha_1)&-A^2\cos(\omega_2t+\alpha_2)&+A^3\cos(\omega_3t-\alpha_3)\end{array} \right)\)
soit :
\(\psi^1=A^1\cos(\omega_1t+\alpha_1)+A^2\cos(\omega_2t+\alpha_2)+A^3\cos(\omega_3t+\alpha_3)\)
\(\psi^2=\sqrt2A^1\cos(\omega_1t+\alpha_1)-\sqrt2A^3\cos(\omega_3t+\alpha_3)\)
\(\psi^3=A^1\cos(\omega_1t+\alpha_1)-A^2\cos(\omega_2t+\alpha_2)+A^3\cos(\omega_3t+\alpha_3)\)
La forme générale de la solution constitue une famille de solutions par le jeu des 6 paramètres qui interviennent : \(A^1, a_1 , A^2, a_2 , A^3, a_3\).
Si on connait exactement les conditions initiales de position et de vitesse de chacune des 3 masses, on obtient ainsi 6 relations qui permettent de déterminer exactement ces 6 paramètres, et donc de spécifier la solution particulière consécutive à ces conditions initiales.
Conditions initiales :
Sachant que \(\psi=M.\phi\) , la condition sur les vitesses initiales \(\psi'=0\) est satisfaite si \(\phi'=0\) en \(t=0\)
Ce qui permet de rechercher à satisfaire cette relation en faisant :
\(\sin(\omega_it+\alpha_i)=0\) en \(t=0\) et donc en faisant \(\alpha_i=0\) \(\forall i\).
Alors, les conditions initiales de position des 3 masses (fixées dans l'énoncé) donnent à l'instant initial \(( t=0 )\) :
\(\Rightarrow \psi_{t=0}=\left(\begin{array}{c} \psi^1 \\ \psi^2 \\ \psi^3 \end{array} \right)_{t=0}= \left(\begin{array}{ccc} A^1&+A^2&+A^3\\\sqrt2A^1&0&-\sqrt2A^3 \\A^1&-A^2&+A^3 \end{array} \right)=\left(\begin{array}{c} 0\\ 1 \\ 0\end{array} \right)\)
On résoud ce système (par exemple en faisant \(\psi^1+\psi^3=0\) et \(\psi^1-\psi^3=0\))
On trouve alors : \(A^2=0\) et \(A^1=\frac{1}{2\sqrt2}=-A^3\)
Noter que \(A^2 = 0 \Rightarrow\) la contribution du mode 2 est nulle (le mode symétrique n'intervient pas, car les conditions initiales ne satisfont pas cette symétrie).
Expression des solutions \(\Rightarrow \psi^1(t)=\frac{1}{2\sqrt2}(\cos\omega_1t-\cos\omega_3t)\)
\(\psi^2(t)=\frac{1}{2}(\cos\omega_1t+\cos\omega_3t)\)
\(\psi^3(t)=\frac{1}{2\sqrt2}(\cos\omega_1t-\cos\omega_3t)\)
On peut encore transformer les sommes de fonctions trigonométrique. en produit pour faire apparaître la solution en forme de battements.
On pose : \(\omega=\frac{\omega_1+\omega_3}{2}\) et \(\omega=\frac{\omega_1-\omega_3}{2}\)
\(\psi^1(t)=\frac{1}{\sqrt2}\sin\omega t\sin\Omega t\)
\(\psi^2(t)=\cos\omega t\cos\Omega t\)
\(\psi^3(t)=\frac{1}{\sqrt2}\sin\omega t\sin\Omega t\)
En reportant les valeurs trouvées pour les pulsations propres, on trouve :
\(\Omega=\frac{\omega_1+\omega_3}{2}=\frac{\sqrt{2-\sqrt2}+\sqrt{2+\sqrt2}}{2}\omega_0\simeq\textrm{1,31} \omega_0 \quad T=\frac{2\pi}{\Omega}=\frac{2\pi}{\textrm{1,31}\omega_0}\)
\(\omega=\frac{\omega_3-\omega_1}{2}=\frac{\sqrt{2+\sqrt2}-\sqrt{2-\sqrt2}}{2}\omega_0\simeq\textrm{0,54} \omega_0 \quad \tau=\frac{2\pi}{\omega}=\frac{2\pi}{\textrm{0,54} \omega_0}\approx\textrm{2,4}T\)
Annexe : détermination des directions propres.
Détermination de \(M_1\) avec \(-2+u^2_1=\sqrt2\)
\(\left(\begin{array}{ccc} -2+u^2&1&0\\ 1&-2+u^2&1 \\ 0&1&-2+u^2 \end{array} \right)\left(\begin{array}{c} 1\\ a_1\\b_1\end{array} \right)=\left(\begin{array}{ccc} -\sqrt2&1&0\\ 1&-\sqrt2&1 \\ 0&1&-\sqrt2 \end{array} \right)\left(\begin{array}{c} 1\\ a_1\\b_1\end{array} \right)=\left(\begin{array}{ccc} -\sqrt2+a_1\\ 1-\sqrt2a_1+b_1 \\ a_1-\sqrt2b_1 \end{array} \right) = \left(\begin{array}{c}0\\ 0\\0 \end{array} \right)\)
\(\Rightarrow a_1=\sqrt{2} \textrm{ et }b_1=0 \Rightarrow M_1=\left(\begin{array}{c} 1\\ \sqrt{2}\\1 \end{array} \right)\)
Détermination de \(M_2\) avec \(u^2_2=2\)
\(\left(\begin{array}{ccc} -2+u^2&1&0\\ 1&-2+u^2&1 \\ 0&1&-2+u^2 \end{array} \right)\left(\begin{array}{c} 1\\ a_2\\b_2\end{array} \right)=\left(\begin{array}{ccc} 0&1&0\\ 1&0&1 \\ 0&1&0 \end{array} \right)\left(\begin{array}{c} 1\\ a_2\\b_2\end{array} \right)=\left(\begin{array}{ccc} a_2\\ 1+b_2 \\ b_2 \end{array} \right) = \left(\begin{array}{c}0\\ 0\\0 \end{array} \right)\)
\(\Rightarrow a_2=0 \textrm{ et }b_2=-1 \Rightarrow M_2=\left(\begin{array}{c} 1\\ 0\\-1 \end{array} \right)\)
Détermination de \(M_3\) avec \(-2+u_3^2=\sqrt2\)
\(\left(\begin{array}{ccc} \sqrt2&1&0\\ 1&\sqrt2&1 \\ 0&1&\sqrt2 \end{array} \right)\left(\begin{array}{c} 1\\ a_3\\b_3\end{array} \right)=\left(\begin{array}{c} \sqrt2+a_3\\ 1+\sqrt2a_3+b_3 \\ a_3+\sqrt2b_3 \end{array} \right) = \left(\begin{array}{c}0\\ 0\\0 \end{array} \right)\)
\(\Rightarrow a_3=-\sqrt2\) et \(b_3=1 \Rightarrow M_3=\left(\begin{array}{c} 1\\ -\sqrt2 \\ 1 \end{array} \right)\)
\(\Rightarrow M=(M_1, M_2, M_3)=\left(\begin{array}{ccc} 1&1&1\\\sqrt2&0&-\sqrt2 \\1&-1&1 \end{array} \right)\)