Pendule à ressort
Partie
Question
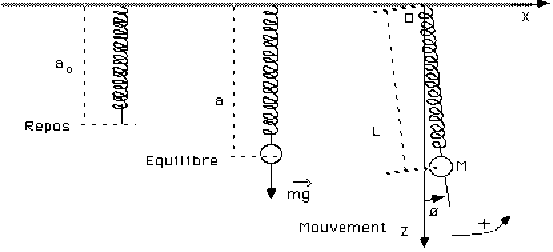
Le schéma ci-dessus représente un pendule dont on étudie le mouvement dans le plan vertical \(( X ~O ~Z)\).
On suppose que le ressort de suspension (de longueur au repos = \(a_0\) ) a une masse nulle et un coefficient de dureté \(K\) assez faible pour que, lorsque la masse \(m\) est à l'équilibre, son allongement par rapport au repos \((a - a_0)\) ne puisse pas être considéré comme négligeable par rapport à la longueur \(a\).
L'origine \(O\) étant prise au point de suspension du pendule et l'orientation positive des angles étant celle indiquée sur le schéma :
On notera \(x\) et \(z\) les coordonnées du point \(A\) de \(OM\) tel que \(OA= a_0\).
Les coordonnées du point \(M\) (la masse \(m\) est supposée ponctuelle) seront notées \(X\) et \(Z\).
On notera \(\psi^1\), \(\psi^2\) les coordonnées de \(M\) par rapport au référentiel centré sur la position au repos (i.e. pour un allongement nul du ressort).
On limitera cette étude au cas des petites oscillations et on admettra que :
\(\frac{X}{a} \textrm{ et } \frac{Z-a}{a}\) sont des infiniment petits du premier ordre, et \(\cos \theta\simeq1\) ( au second ordre près)
1- Exprimer (en fonction de \(X\), \(x\), \(\psi^1\), \(\psi^2\)) les composantes \(T_x\) et \(T_z\) de la force de tension agissant sur \(M\). En déduire, en projection sur ces axes, l'expression du principe fondamental de la dynamique.
2- En posant \(\psi^1 = X\) et \(\psi^2 = Z - a\) et en utilisant les approximations (d'ordre 2) consécutives aux petites oscillations, exprimer sous forme matricielle le système différentiel régissant le mouvement de \(M\) dans le système de coordonnées (\(\psi^1\),\(\psi^2\)).
3- En déduire les modes propres ainsi que l'expression de la vibration périodique la plus générale dans le cadre de ces approximations.
Rappel de cours
Voir la page Mise en équations
Solution détaillée
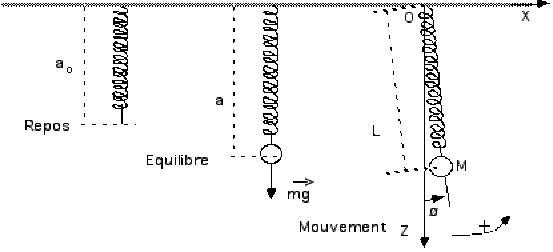
1-
\(\overrightarrow{OA} \left|\begin{array}{l} x \\ z \end{array} \right. \qquad\qquad \overrightarrow{OM} \left|\begin{array}{l} X=\psi^1 \\ Z=\psi^2+a \end{array}\right.\)
\(||\overrightarrow{OA}||=a_o\qquad\qquad ||\overrightarrow{OM}||=L\)
\(||\overrightarrow{OM_0}||=a\)
\(\overrightarrow T=K\overrightarrow{MA} \left|\begin{array}{l} K(x-X)=T_x \\ K(z-Z)=T_z \end{array}\right.\)
\(\overrightarrow T+M\overrightarrow g=m\overrightarrow{\gamma}\Rightarrow \begin{array}{ll} K(x-X)=m\ddot X & (a) \\ K(z-Z)+mg=m\ddot z & (b) \end{array}\)
2-
\(mg=K(a-a_0)\)[remarquer les sens \(>0\) :\(a>a_0\) et \(g>0\)]
\(z=a_0\cos \theta\simeq a_0\) (ordre 2 près)
\(\Rightarrow K(z-Z)+mg=K(a_0-Z)+K(a-a_0)=K(a-Z)=-K\psi^2\)
\((b) \Rightarrow-K\psi^2=m\ddot Z=m\ddot{\psi}^2\Rightarrow \ddot{\psi}^2=\frac{K}{m}\psi^2\) (à l'ordre 2 près)
\(x=a_0\sin\phi\) (relation algébrique)
\(x=a_o\frac{X}{L} \Rightarrow x-X=-X(1-\frac{a_0}{L})\)
Notons \(\Delta L = L - a\) la variation de longueur (par rapport à l'équilibre) que l'on suppose (par rapport à \(L\)) être infiniment petit du 1er ordre (petites oscillations)
\(\Delta=\frac{1}{L}=\frac{1}{L^2}\Delta L\)
(car \(\Delta\frac{1}{L}=-\frac{1}{L}\frac{\Delta L}{L})\)
\(\Rightarrow 1- \frac{a_0}{L}\simeq1-\frac{a_0}{a}\)
\(\Rightarrow\) la variation de \(\frac{1}{L}\) est de l'ordre 2 si \(L\) est infiniment grand par rapport à \(\Delta L\)
\(\Rightarrow \frac{1}{L}=\frac{1}{L}-\frac{1}{a}\simeq0\) (à l'ordre 2 près)
\(\Rightarrow x-X\simeq-X(1-\frac{a_0}{a}) \stackrel{(a)}{\Rightarrow} m\ddot X=-K(1-\frac{a_0}{a})X\)
On peut simplifier cette expression en remarquant que :
\((1-\frac{a_0}{a})=\frac{a-a_0}{a}\) avec \(K(a-a_0)=mg \Rightarrow m\ddot X=-\frac{mg}{a}X\) soit \(\ddot{\psi}^1=-\frac{g}{a}\psi^1\)
Au 2ème ordre près, le système s'écrit donc : \(\left(\begin{array}{c} \ddot{\psi}^1 \\ \ddot{\psi}^2 \end{array} \right)=\left(\begin{array}{cc} -\frac{g}{a}&0 \\ 0&-\frac{K}{m} \end{array} \right) \left(\begin{array}{c} \psi^1 \\ \psi^2 \end{array} \right)\)
les pulsations sont respictivement : \(\begin{array}{l} \omega_1\Leftarrow \omega_1^2=\frac{g}{a} \\ \omega_2 \Leftarrow \omega_2^2=\frac{K}{m} \end{array}\)
\(\Rightarrow \begin{array}{l} \sin X=\textrm{projection d'un mouvement pendulaire} \\ \sin Z= \textrm{mouvement d'oscillation (de faible amplitude) déterminé par la raideur du ressort} \end{array}\)
Remarque : Si on faisait une autre hypothèse :
petites oscillations selon \(X\) (i.e en \(\theta\)) mais :
oscillations selon l'axe \(Z\) non négligeables devant \(a\) on aurait un autre système.
En effet : l'équation en \(\psi^2\) serait alors inchangée, mais par contre : \(K(x-X)=K(a_0\sin \theta -L\sin \theta)=K\sin \theta(a_0-L)\)
\(=-\sin \theta[K(a-a_0)+K(L-a)]\)
\(=-\sin \theta[mg+K(L\cos \theta-a)]\) (à l'ordre 2 près)
\(=- \sin \theta[mg+K\psi^2]\) et \(\sin\theta\simeq \tan\theta\simeq\frac{X}{L\cos\theta}\simeq\frac{X}{a+4}\)
\(\Rightarrow K(x-X)\simeq-X[\frac{mg}{a+\psi^2}+\frac{K\psi^2}{a+\psi^2}]=m\ddot X\)
\(\ddot X\simeq-(\frac{g}{a+\psi^2}+\frac{K\psi^2}{m(a+\psi^2)})X\) que l'on ne sait pas résoudre comme ça.
\(\psi=\Sigma ~a_i ~M_i ~\cos(\omega_i t+\varphi_i)\) (avec \(\varphi_i=0 ~\forall i \))
\(\psi=\underbrace{\frac{a}{3}(\sqrt3+2)M_1\cos(\omega_1t)}_{\psi_1}+\underbrace{\frac{a}{3}M_3 \cos(\omega_3t)}_{\psi_3}+\underbrace{\frac{a}{3} (2-\sqrt3)M_5\cos(\omega_5t)}_{\psi_5}\)
avec : \(M_1 : \left(\begin{array}{c} \frac{1}{2} \\ \frac{\sqrt3}{2} \\ 1 \\ \frac{\sqrt3}{2} \\ \frac{1}{2} \end{array} \right) \qquad M_3 : \left(\begin{array}{c} 1\\ 0 \\ -1 \\ 0\\ 1 \end{array} \right) \qquad M_5 : \left(\begin{array}{c} \frac{1}{2} \\ -\frac{\sqrt3}{2} \\ 1 \\ -\frac{\sqrt3}{2} \\ \frac{1}{2} \end{array} \right)\)
\(\left|\begin{array}{l} \frac{a_5}{a_1}=\frac{2-\sqrt3}{2+\sqrt3} \\ \frac{a_3}{a_1}=\frac{1}{2+\sqrt3} \end{array} \right.\)