Pendules
Partie
Question
A- Pendule sphérique.
Le pendule sphérique est représenté ci-contre.
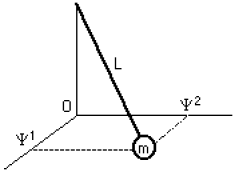
On admettra que la masse n'effectue que des petites oscillations, de sorte que son mouvement a lieu, en première approximation, dans un plan horizontal. Dans ce plan horizontal, la position de la masse \(m\) est repérée par ses coordonnées\( \psi^{1}\) et \(\psi^{2}\) .
Exprimer les relations fondamentales de la dynamique sous forme matricielle : \(\ddot{\psi}=U.\psi\)
Résoudre ce système.
Interpréter la nature des solutions.
B- Pendule double plan.
Le pendule double plan est représenté ci-contre
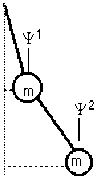
On admettra que la masse n'effectue que des petites oscillations, de sorte que le mouvement de chacune des masses a lieu, en première approximation, dans un même plan vertical et selon une direction horizontale. Dans ce plan vertical, la position des masses \(m\) est repérée par leurs coordonnées respectives \(\psi^{1}\) et \(\psi^{2}\) .
Exprimer les relations fondamentales de la dynamique sous forme matricielle : \(\ddot{\psi}=U.\psi\)
Résoudre ce système.
Interpréter la nature des solutions.
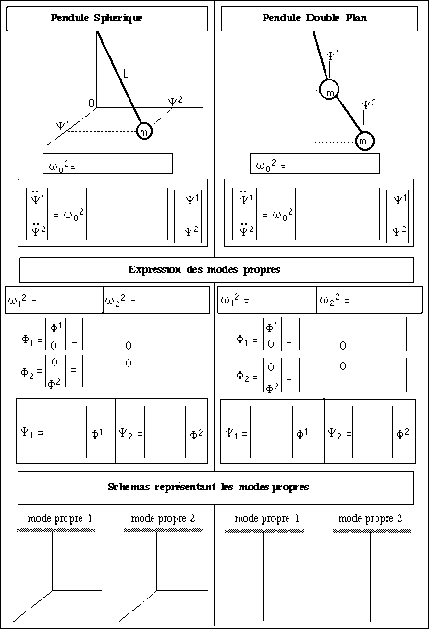
C- Tableaux Récapitulatifs (à compléter).
Aide simple
A- Pendule sphérique
Noter que :
on se limite aux "petites oscillations"
le fait que le pendule soit "sphérique" se traduit par le fait que si l'on projette l'oscillation dans deux plans verticaux orthogonaux, il n'y a pas de couplage entre ces deux projections, et ces oscillations projetées ont même fréquence.
toutes les projections sont algébriques.
B- Pendule double plan
Noter que :
on se limite aux "petites oscillations"
le fait que le pendule soit "plan" signifie que l'oscillation peut se projeter dans ce plan vertical
il y a un couplage entre les oscillations de chacune des masses
toutes les projections sont algébriques.
Rappel de cours
Voir la page Mise en équations
Solution détaillée
A- Pendule sphérique
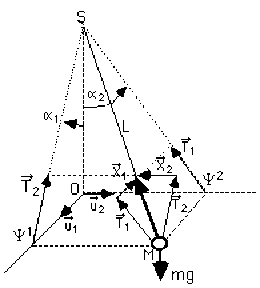
Le mouvement général du pendules sphérique (représenté ci-dessus) s'inscrit sur une sphère de rayon \(L\) et de centre \(S\). Ce mouvement peut se projeter sur les 2 plans verticaux \((SO\psi^1)\) et \((SO\psi^2)\).
La projection du mouvement général sur chacun des 2 plans verticaux est bien sûr un mouvement plan possible pour le pendule.
Dans le cas particulier où la masse n'effectue que des petites oscillations, son mouvement a lieu en première approximation, dans le plan horizontal \((\psi^1 O \psi^2)\) et ce mouvement se décompose alors simplement sur \(\overrightarrow{u_1}\) et \(\overrightarrow{u_2}\).
Pour projeter sur \(\overrightarrow{u_1}\) et \(\overrightarrow{u_2}\) la tension \(\overrightarrow T\) (portée par MS), on peut remarquer que :
\(\overrightarrow T=\overrightarrow{T_1}+\overrightarrow{X_1}=\overrightarrow{T_2}+\overrightarrow{X_2}\) où : \(\overrightarrow{X_1} \parallel \overrightarrow{u_1}\) et \(\overrightarrow{T_1} \perp \overrightarrow{u_1}\), \(\overrightarrow{X_2}\parallel \overrightarrow{u_2}\) et \(\overrightarrow{T_2} \perp \overrightarrow{u_2}\)
on voit alors que : \(\overrightarrow T.\overrightarrow{u_2}=(\overrightarrow{T_1}+\overrightarrow{X_1})\) .\(\overrightarrow{u_2}=\overrightarrow{T_1}.\overrightarrow{u_2}\) et : \(\overrightarrow T.\overrightarrow{u_1}=(\overrightarrow{T_2}+\overrightarrow{X_2}).\overrightarrow{u_1}=\overrightarrow{T_2}.\overrightarrow{u_1}\)
\(a_1\) et \(a_2\) petits \(\Rightarrow ||\overrightarrow T||\cong||\overrightarrow{T_1}||\cong||\overrightarrow{T_2}||\Rightarrow\) le PFD en projection sur \(\overrightarrow{u_1}\) et \(\overrightarrow{u_2}\) donne : \(m~\ddot{\psi}^1=\overrightarrow T.\overrightarrow{u_1}\) avec :
\(\overrightarrow T.\overrightarrow{u_1}=-T_2\sin\alpha_1\cong-T\frac{\psi^1}{L}\Rightarrow \ddot{\psi}^1=-\frac{T}{L}\psi^1\)
et : \(m~\ddot{\psi}^2=\overrightarrow T.\overrightarrow{u_2}\) avec : \(\overrightarrow T.\overrightarrow{u_2} =-T_1\sin\alpha_2\cong-T\frac{\psi^2}{L} \Rightarrow \ddot{\psi}^2=-\frac{T}{L}\psi^2\).
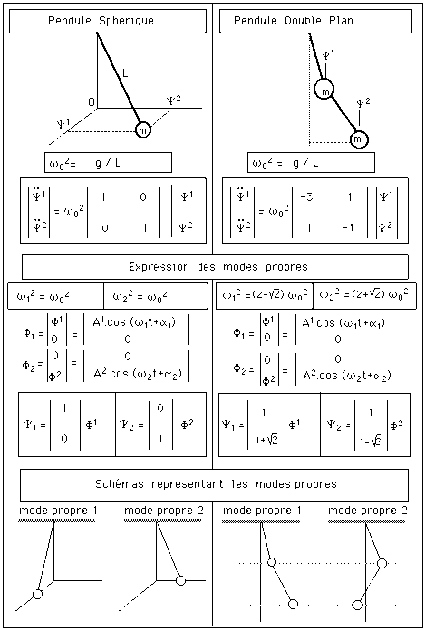
On posera \(\omega_0^2=\frac{T}{L}\)
Ces 2 relations s'expriment sous forme matricielle : \(\ddot{\psi}=U\psi\) avec \(\psi=\left|\begin{array}{c} \psi^1 \\ \psi^2 \end{array}\right|\)
et : \(U=-\frac{T}{L} \left(\begin{array}{cc} 1&0 \\ 0&1 \end{array}\right)=-\omega_0^2\left(\begin{array}{cc} 1&0 \\ 0&1 \end{array}\right)\).
Remarquer que dans le cas d'oscillations d'amplitudes relativement importantes devant \(L\), la tension \(T\) n'est pas constante (la tension est fonction de la vitesse, qui est maximum lorsque le pendule passe par la verticale, et minimale lorsque le pendule arrive à sa hauteur maximale). Dans ce cas là, on ne peut pas résoudre ce système par cette méthode.
Par contre, dans le cas d'oscillations de faible amplitude par rapport à \(L\), on admettra que la norme \(T\) de la force de tension reste constante au cours du mouvement, et égale à sa valeur à l'équilibre, à savoir \(T = mg/L\).
Dans ces conditions, les 2 équations ci-dessus sont linéaires, et ont pour solution immédiate :
\(\psi^1=A^1\cos(\omega_0t+\alpha_1)\) et \(\psi^2=A^2\cos(\omega_0t+\alpha_2)\)
Le mode 1 de vibration est alors : \(\psi_1=\left|\begin{array}{c} \psi^1 \\ 0 \end{array}\right|\) et le mode 2 : \(\psi_2=\left|\begin{array}{c} 0 \\ \psi^2 \end{array}\right|\)
(mouvements plans)
et la vibration générale s'exprime comme combinaison linéaire des modes \(\psi_1\) et \(\psi_2\)
soit : \(\psi=\psi_1+\psi_2=\left|\begin{array}{c} \psi^1 \\ \psi^2 \end{array}\right|\)
Remarquer que la matrice \(U\) est diagonale, ce qui signifie que les équations en \(\psi_1\) et \(\psi_2\) sont indépendantes : on dit qu'elles sont découplées. Dans ce cas, on peut alors les résoudre indépendamment.
B- Pendule double plan
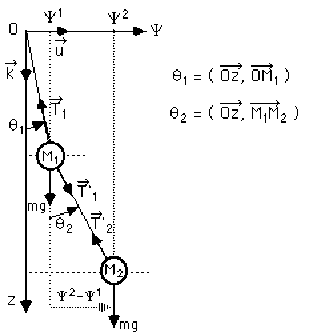
\(\cos(\overrightarrow u\overrightarrow{T_1})=\cos(\frac{\pi}{2}+\theta_1)=-\sin(\theta_1), \cos(\overrightarrow k\overrightarrow{T_1})=\cos(\pi+\theta_1)=-\cos(\theta_1)\)
\(\cos(\overrightarrow u\overrightarrow{T'_1})=\cos(-\frac{\pi}{2}+\theta_2)=\cos(\frac{\pi}{2}-\theta_2)=\sin(\theta_2), \cos(\overrightarrow k\overrightarrow{T'_1})=\cos(\theta_2)\)
\(\cos(\overrightarrow u\overrightarrow{T_2})=\cos(\frac{\pi}{2}+\theta_2)=-\sin(\theta_2), \cos(\overrightarrow k\overrightarrow{T'_2})=\cos(\pi+\theta_2)=-\cos(\theta_2)\)
En notant \(\psi^1\) et \(\psi^2\) les coordonnées respectives de \(M^1\) et \(M^2\) sur l'axe \(\overrightarrow u\) , et en projetant le PFD sur les vecteurs unitaires \(\overrightarrow u\) et \(\overrightarrow k\), on obtient :
\(\begin{array} {lll} \textrm{sur } \overrightarrow u \Rightarrow \quad (1) \quad \overrightarrow u.\overrightarrow{T_1}+\overrightarrow u.\overrightarrow{T'_1}=m\ddot{\psi}^1 \quad &(3)& \quad \overrightarrow u.\overrightarrow{T'_2}=m\ddot{\psi}^2 \\ \textrm{sur } \overrightarrow k \Rightarrow \quad (2) \quad \overrightarrow k.\overrightarrow{T_1}+\overrightarrow k.\overrightarrow{T'_1}+mg=m\ddot z^1 \quad &(4)& \quad \overrightarrow k.\overrightarrow{T'_2}+mg=m\ddot z^2 \end{array}\)
\((1) \Rightarrow \quad ||\overrightarrow{T_1}||.(-\sin\theta_1)+||\overrightarrow{T'_1}||\sin\theta_2=m\ddot{\psi}^1\)
\((2) \Rightarrow \quad ||\overrightarrow{T_1}||.(-\cos\theta_1)+||\overrightarrow{T'_1}||\cos\theta_2+mg=m\ddot z^1\)
\((3) \Rightarrow \quad ||\overrightarrow{T'_2}||.(-\sin\theta_2)=m\ddot{\psi}^2\)
\((4)\Rightarrow \quad ||\overrightarrow{T'_2}||.(-\cos\theta_2)+mg=m\ddot z^2\)
On élimine les fonctions trigonométriques : \(\sin\theta_1=\frac{\psi^1}{L}\sin\theta_2=\frac{\psi^2-\psi^1}{L}\)
et, dans l'approximation des petites oscillations : \(\cos\theta_1\approx1, \cos\theta_2\approx1\)
On admettra que, dans cette approximation, le mouvement de chaque masse se produit dans un plan horizontal : \(\ddot z^1=0 \quad \ddot z^2=0\)
Alors, \(\begin{array}{ll} &(4) \Rightarrow ||\overrightarrow{T'_2}||(-\cos\theta_2)+mg\approx0\Rightarrow ||\overrightarrow{T'_1}||=||\overrightarrow{T'_2}||\approx mg \\ &(2) \Rightarrow-||\overrightarrow{T_1}||+||\overrightarrow{T'_1}||+mg\approx0\Rightarrow ||\overrightarrow{T_1}||\approx2mg \end{array}\)
En reportant ces valeurs dans (1) \(\Rightarrow -2mg\frac{\psi^1}{L}+mg\frac{\psi^2-\psi^1}{L}=m\ddot{\psi}^1\) et dans (3)\(\Rightarrow -mg\frac{\psi^2-\psi^1}{L}=m\ddot{\psi}^2\)
\(\frac{g}{L}\) étant homogène au carré d'une pulsation, on pose \(\frac{g}{L}=\omega_0^2\)
\(\Rightarrow \begin{array}{ll} (5) &\ddot{\psi}^1=\omega_0^2(-3\psi^1+\psi^2) \\ (6) & \ddot{\psi}^2=\omega_0^2(\psi^1-\psi^2) \end{array}\)
Ces relations s'expriment sous forme matricielle : \(\ddot{\psi}=U\psi\) avec \(U=\left(\begin{array}{cc} -3&1 \\ 1&-1 \end{array}\right)\)
Rappel de la méthode :
Le problème est de passer :
de la relation \(\ddot{\psi}=U . \psi\) dans laquelle la matrice \(U\) du système n'est pas diagonale
à une relation du type \(\ddot{\phi}=U_d . \phi\) dans laquelle la matrice \(U_d\) sera diagonale, de sorte que cette relation puisse se résoudre facilement.
Pour résoudre cette équation en coordonnées \(\phi\), on posera par exemple : \(U_d=\left(\begin{array}{cc} -\omega_1^2&0 \\ 0&-\omega_2^2 \end{array}\right)\)
et il suffira de développer l'équation matricielle précédente pour obtenir deux équations différentielles indépendantes en coordonnées \(\phi\) :
\(\ddot{\phi}^1=-\omega_1^2\phi^1, \quad \ddot{\phi}^2=-\omega_2^2\phi^2\)
Les solutions en coordonnées \(\phi\) sont :
\(\phi_1=\left|\begin{array}{c} \phi^1 \\ 0 \end{array}\right|\) et \(\phi_2=\left|\begin{array}{c} 0 \\ \phi^2 \end{array}\right|\) avec \(\begin{array}{l} \phi^1=A^1\cos(\omega_1t+\alpha_1) \\ \phi^2=A^2\cos(\omega_2t+\alpha_2) \end{array}\)
La méthode générale consiste donc à trouver la matrice \(M\) de changement de base, telle que soit :
\(\phi \stackrel{M}{\longrightarrow} \psi \Leftrightarrow \psi=M.\phi\)
\(\substack{{\phi \longleftarrow \psi }\\ M^{-1}} {\Leftrightarrow \phi=M^{-1}\psi}\)
\(\begin{array}{ll} &\psi=M.\phi \\ &\Downarrow \\ \ddot{\psi}=U.\psi \Rightarrow &\ddot{\psi}=U.M.\phi \\ &\Downarrow \\ \phi=M^{-1}.\psi \Rightarrow &\ddot{\phi}=M^{-1}.\ddot{\psi}=M^{-1}.U.M.\phi \end{array}\)
Le problème est donc résolu si l'on sait trouver une matrice de changement de base M telle que la matrice \(M ^{-1}.U. M\) soit diagonale. On posera alors : \(M^{ -1}.U. M = U_d\)
En multipliant à gauche cette relation matricielle par \(M\), on voit que :
\(U_d=M^{-1}.U.M \Leftrightarrow MU_d=UM\)
avec : \(U_d=\left(\begin{array}{cc} -\omega_1^2&0 \\ 0&-\omega_2^2 \end{array}\right) \quad \Rightarrow MU_d=(-\omega_1^2M_1, -\omega_2^2M_2)\)
En posant que la matrice \(M\) est constituée des vecteurs \(M_1\) et \(M_2\) , soit : \(M = (M_1, M_2)\), on voit que \(UM = (UM_1, UM_2)\)
Donc :
\(U_d=M^{-1}UM \Leftrightarrow \begin{array}{lll} (7)& UM_1=-\omega_1^2M_1 & \omega_1 \textrm{ et } \omega_2 \textrm{ sont les pulsations propres} \\ (8) &UM_2=-\omega_2^2M_2 & \omega_1 \textrm{ et }\omega_2 \textrm{ sont les directions propres} \end{array}\)
Résolution :
Pour résoudre l'équation \(U. M_i = - \omega_i^2. M_i\), on cherche les racines de : \(\textrm{d\'et}( U + \omega_i^2I ) = 0\)
où I est la matrice unité.
On posera pour faciliter le calcul : \(\omega_1=\lambda_1\omega_0\) et \(\omega_2=\lambda_2\omega_0\) (\(\lambda_1\) et \(\lambda_2>0)\)
\(\Rightarrow \textrm{d\'et}\left(\begin{array}{cc} -3+\lambda^2&1 \\ 1&-1+\lambda^2\end{array}\right)=0 \Rightarrow \begin{array}{l} \lambda_1^2=2-\sqrt2 \\ \lambda_2^2=2+\sqrt2 \end{array}\)
On voit d'après les équations (7) et (8) que les "vecteurs propres" \(M_i=\left(\begin{array}{c} M_i^1 \\ M_i^2\end{array}\right)\) ne peuvent être déterminés qu'à un coefficient multiplicatif près (raison pour laquelle l'appellation "directions propres" est plus correcte).
En général, on pourra donc poser arbitrairement : \(M_1=\left|\begin{array}{c} 1 \\ M_1^1\end{array}\right|\) et \(M_2=\left|\begin{array}{c} 1 \\ M_2^1\end{array}\right|\)
En portant dans les équations (7) et (8), on trouve : \(M_1=\left|\begin{array}{c} 1 \\ 1+\sqrt2\end{array}\right|\) et \(M_2=\left|\begin{array}{c} 1 \\ 1-\sqrt2\end{array}\right|\)
La vibration générale du pendule double plan est donc représentée par le vecteur d'état :
\(\psi=M\phi=(M_1, M_2) \left|\begin{array}{c} \phi^1 \\ \phi^2\end{array}\right|=M_1\phi^1+M_2\phi^1=\psi_1+\psi_2\)
\(\psi_1\) : mode propre 1
\(\psi_2\) : mode propre 2
En résumé, les modes propre sont définis (à un coefficient multiplicatif près) par :
\(\psi_1=M_1\phi^1=A^1 \left|\begin{array}{c} 1 \\ 1+\sqrt2\end{array}\right|\cos(\omega_1t+\alpha_1)\)
\(\psi^2=M_2\phi^2=A^2 \left|\begin{array}{c} 1 \\ 1-\sqrt2\end{array}\right|\cos(\omega_2t+\alpha_2)\)
Remarques :
Dans un mode propre \(i\), toutes les masses constituant le système vibrent selon la même fonction propre \(\phi^i\) , et avec des rapports d'amplitudes déterminés par les composantes du vecteur propre \(M_i\) .
Il peut arriver qu'un mode propre soit tel que l'une des composantes reste nulle, par exemple justement la composante qu'on a posé arbitrairement égale à 1 ( ici : \(M_1^1\), ou \(M_2^1\)).
Bien entendu, on s'en apercevra en tombant sur une impossibilité à résoudre les équations...
C- Tableaux récapitulatifs
Les schémas représentant les modes propres du pendule double sont reportés dans le tableau récapitulatif.