Système 5 masses - 6 ressorts
Partie
Question
On considère un système constitué de 5 masses identiques \(m\) reliées entre elles et aux extrémités du système par des ressorts identiques de dureté \(K\). Elles sont assujetties à un mouvement transversal, par un guidage sans frottement situé dans un même plan horizontal.
Par le calcul direct de \(\textrm{d\'et } [ U + \omega^2I ] = 0\), déterminer les pulsations propres \(\omega_1\) et \(\omega_2\) du système. (on les numérotera par ordre de valeurs croissantes).
Vérifier ces valeurs en appliquant au cas \(N=5\) l'expression générale trouvée dans le cas de \(N\) masses.
Déterminer par le calcul direct le vecteur propre \(M_1\).
Vérifier les valeurs de ses composantes en utilisant l'expression générale des vecteurs propres appliquée à ce cas \(N= 5\). De cette même façon, déterminer l'ensemble des vecteurs propres du système.
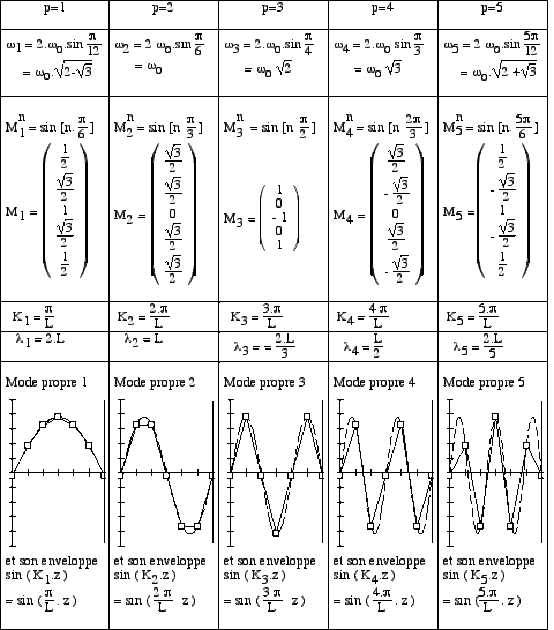
Pour l'ensemble des modes propres, représenter sur un tableau récapitulatif les valeurs de \(\omega_p\), \(M_p\), \(K_p\), \(l_p\) et dessiner ces modes propres.
Écrire l'expression générale de la vibration du système.
Donner une expression particulière de la vibration dans le cas où la vitesse initiale de chacune des masses est nulle.
Dans ce cas, montrer que si l'état initial possède une symétrie du type \(\psi^1 = \psi^5\) et \(\psi^2 = \psi^4\) alors la vibration s'exprimera uniquement sur les modes 1, 3, et 5 .
En supposant de plus que dans l'état initial toutes les masses ont la même amplitude initiale, en déduire les composantes de la vibration sur la base de ces modes propres.
Rappel de cours
Voir la page Mise en équations
Solution détaillée
1- Le système que l'on étudie ici est constitué de 5 masses identiques (\(m\)) reliées entre elles et reliées aux extrémités du système par des ressorts identiques de dureté \(K\).
Les masses sont assujetties à un mouvement transversal, par un guidage sans frottement situé dans un même plan horizontal. Ce système est de même type que celui de l'exercice 8.
Le PFD appliqué à la masse de rang \(n\) :
\(m . \ddot{\psi}^n=\frac{T}{a} (\psi^{n+1}-\psi^n)-\frac{T}{a}(\psi^n-\psi^{n-1})\)
Dans cette équation, \(\psi^0\) et \(\psi^6\) représentent les extrémités du système. Les extrémités étant fixes, tout se passe donc comme si en \(n=0\) et en \(n=6\) on avait des masses immobiles :
\(\psi^0=\psi^6=0\).
Cette remarque permet d'utiliser l'expression générale ci-dessus y compris pour la première et pour la dernière masse.
Par exemple, en faisant dans cette équation \(n=1\) et \(\psi^0 = 0\)
\(\Rightarrow m . \ddot{\psi}^1=\frac{T}{a} (\psi^2-\psi^1)-\frac{T}{a}\psi^1\)
Avec \(\omega_0^2=\frac{T}{m . a}\), on obtient la matrice du système :
\(U=\omega_0^2 . \left(\begin{array}{ccccc} -2&1&0&0&0 \\ 1&-2&1&0&0 \\ 0&1&-2&1&0 \\ 0&0&1&-2&1 \\ 0&0&0&1&-2 \end{array} \right)\)
On pose \(\omega=\Omega \omega_0\), où \(\Omega\) est un coefficient sans dimension.
On résoud :
\(\textrm{d\'et }[U+\omega^2I]=\textrm{d\'et }\left(\begin{array}{ccccc} -2+\Omega^2&1&0&0&0 \\ 1&-2+\Omega^2&1&0&0 \\ 0&1&-2+\Omega^2&1&0 \\ 0&0&1&-2+\Omega^2&1 \\ 0&0&0&1&-2+\Omega^2 \end{array} \right)=0\)
En développant ce déterminant d'ordre 5, on peut l'exprimer en fonction de celui d'ordre 4 et de celui d'ordre 3. En posant \((-2+\Omega^2) = a\), on obtient :
\(\textrm{d\'et }(u_2)=a^2-1\)
\(\textrm{d\'et }(u_3)=a . \textrm{d\'et }(u_2)-\textrm{d\'et }(u_1)=a . (a^2-1)-a=a . (a^2-2)\)
\(\textrm{d\'et }(u_4)=a . \textrm{d\'et }(u3)-\textrm{d\'et }(u_2)=a^2 . (a^2-2)-(a^2-1)\)
\(\textrm{d\'et }(u_5)=a . \textrm{d\'et }(u_4)-\textrm{d\'et }(u_3)=a^3 . (a^2-2)-a(a^2-1)-a . (a^2-2)=a . (a^2-1)(a^2-3)\)
\(\textrm{d\'et }(u_5)=0\Leftarrow a=0\) et \(\Omega^2=2\)
\(\Leftarrow a^2=1\), \(a=\pm 1\), \(\Omega^2=3\)
\(a=-1\), \(\Omega^2=1\)
\(\Leftarrow a^2=3 , a=+\sqrt3\) , \(\Omega^2=2+\sqrt3\)
\(a=-\sqrt3 , \Omega^2=2-\sqrt3\)
En numérotant les pulsations propres par ordre de valeurs croissantes, on obtient :
\(\omega_1=\sqrt{2-\sqrt3} . \omega_0\)
\(\omega_2=\omega_0\)
\(\omega_3=\sqrt2 . \omega_0\)
\(\omega_4=\sqrt3 . \omega_0\)
\(\omega_5=\sqrt{2+\sqrt3} . \omega_0\)
2- L'expression générale trouvée dans le cas de \(N\) masses est : \(\omega_p=2\omega_0\sin\frac{p\pi}{2.(N+1)}\)
Pour \(N=5\), on doit donc évaluer les sinus : \(\sin \frac{p . \pi}{12}\) pour \(p\) de 1 à 5.
On peut pour ce faire utiliser les relations :
\(\sin \frac{x}{2}=\sqrt{\frac{1-\cos x}{2}}\) et \(\cos \frac{x}{2}=\sqrt{\frac{1+\cos x}{2}}\)
Par exemple : \(\cos\frac{\pi}{6}=\sqrt{\frac{1+\cos\frac{\pi}{3}}{2}}=\sqrt{\frac{1+\frac{1}{2}}{2}}=\frac{\sqrt3}{2}\)
\(\sin \frac{\pi}{12}=\sqrt{\frac{1-\cos\frac{\pi}{6}}{2}}=\sqrt{\frac{1-\frac{\sqrt3}{2}}{2}}=\frac{\sqrt{2-\sqrt3}}{2}\)
\(\omega_1=2\omega_0\sin\frac{\pi}{12} \Rightarrow \omega_1=\omega_0\sqrt{2-\sqrt3}\)
Et on procède de la même façon pour les autres pulsations (voir les valeurs dans le tableau récapitulatif).
3- la relation :
\(U.M_i=\omega_0^2\left(\begin{array}{ccccc} -2&1&0&0&0 \\ 1&-2&1&0&0 \\ 0&1&-2&1&0 \\ 0&0&1&-2&1 \\ 0&0&0&1&-2 \end{array} \right)\left(\begin{array}{c} M_i^1 \\ M_i^2 \\M_i^3 \\M_i^4 \\ M_i^5 \end{array} \right)=-\omega_i^2M_i=-\omega_i^2\left(\begin{array}{c} M_i^1 \\ M_i^2 \\M_i^3 \\M_i^4 \\ M_i^5 \end{array} \right)\)
permet de déterminer les pulsations propres \(\omega_i\) et les vecteurs propres \(M_i\) . Par exemple, à l'ordre 1, et en posant \(\omega_i = \Omega_ i .\omega_0\) :
\(-2M_1^1+M_1^2=-\Omega_1^2M_1^1\quad \qquad (1)\)
\(M_1^1-2M_1^2+M_1^3=-\Omega_1^2M_1^2 \quad (2)\)
\(M_1^2-2M_1^3+M_1^4=-\Omega_1^2M_1^3 \quad (3)\)
\(M_1^3-2M_1^4+M_1^5=-\Omega_1^2M_1^4 \quad (4)\)
\(M_1^4-2M_1^5=-\Omega_1^2M_1^5\quad \qquad (5)\) (avec : \(\Omega_1^2=2-\sqrt3\))
On posera arbitrairement l'une des composantes de \(M_i\) égale à 1. On prendra ici \(M_1^3=1\).
La relation \((1) \Rightarrow M_1^2=\sqrt3M_1^1\)
En portant dans (2), avec \(M_1^3=1\Rightarrow M_1^1=\frac{1}{2}\). Avec \((1) \Rightarrow M_1^2=\frac{\sqrt3}{2}\)
En portant dans \((3) \Rightarrow M_1^4=\frac{\sqrt3}{2}\). Avec \((4) \Rightarrow M_1^5=\frac{1}{2}\)
La relation (5) confirme les valeurs trouvées.
On procède de la même façon pour déterminer les composantes des autres vecteurs propres.
4- On retrouve que ces composantes ont une valeur qui satisfait l'expression générale vue en cours qui concerne une système de masses et de ressorts dont les extrémités sont fixes :
\(M_p^n=\sin[n\frac{p\pi}{(N+1)}]\)
Le tableau récapitulatif (-e-) donne les valeurs calculées à partir de cette expression.
Remarquer que, si a est la distance entre 2 masses successives, \((N+1).a\) est égal à la longueur \(L\) du système, et n.a est l'abscisse \(z_n\) de la masse \(n\). Dans ces conditions, \(M_p^n\) peut s'écrire :
\(M_p^n=\sin[\frac{p . \pi}{(N+1). a} . n.a]=\sin[\frac{p . \pi}{L} . n.a] = \sin[K_p . z_n]\)
Remarquer encore que dans un mode quelconque (numéro \(p\)), les amplitudes successives des masses (numérotées par n et données par : \(\sin ~[K_p . z_n]\)) s'inscrivent sur une enveloppe dont l'équation est celle donnée par le \(\sin~[K_p.z]\).
5- Tableau récapitulatif
6- L'expression générale de la vibration du système est : \(\psi=\displaystyle{\sum_{p=1}^{p=5}\psi_p=\sum_{p=1}^{p=5}M_p\phi^p}\).
avec \(\phi^p=A^p\cos(\omega_pt+\alpha_p)\)
expression dans laquelle sont connus les vecteurs propres \(M_p\) et les pulsations propres \(\omega_p\).
Les coefficients \(A^p\) déterminent le "poids" de chacun des modes propres.
Les 5 coefficients d'amplitudes \(A^p\) ainsi que les 5 déphasages \(\alpha_p\) intervenant dans une décomposition particulière sont déterminés, si l'on connait 10 relations particulières concernant la vibration. Par exemple si l'on connaît 10 conditions initiales (5 pour la position et 5 pour la vitesse de chacune des 5 masses).
7- On suppose que la vitesse initiale de chacune des masses est nulle. Sachant que :
\(\psi_p(t)=M_pA^p\cos(\omega_pt+\alpha_p)\Rightarrow \psi'_p(t)=-\omega_pM_pA^p\sin(\omega_pt+\alpha_p)\)
\(\Rightarrow \psi'_p(t=0)=-\omega_pM_pA^p\sin \alpha_p\)
On remarquera que :
vitesse initiale \(=0 (\textrm{en } t=0)\Leftarrow \psi'_p(t=0)=0 ~\forall p\Leftarrow \sin(\alpha_p)=0~\forall p\Leftarrow (\alpha_p)=0 ~\forall p\)
On recherche donc un développement de \(\psi\) satisfaisant la condition : \(\{\alpha_p\}=0 ~\forall p\)
soit : \(\psi=\displaystyle{\sum_{p=1}^{p=5}M_pA^p\cos(\omega_p . t)\Rightarrow \psi=\sum_{p=1}^{p=5}M_pA^p}\) en \(t=0\)
8- Avec ces conditions de vitesses initiales, la position initiale de chacune des masses est donnée à l'instant \(t=0\) par :
\(\psi^1_{(t=0)}=\frac{1}{2}A^1+\frac{\sqrt3}{2}A^2+1A^3+\frac{\sqrt3}{2}A^4+\frac{1}{2}A^5\)
\(\psi^2_{(t=0)}=\frac{\sqrt3}{2}A^1+\frac{\sqrt{3}}{2}A^2+0A^3-\frac{\sqrt3}{2}A^4-\frac{\sqrt3}{2}A^5\)
\(\psi^3_{(t=0)}=A^1+0A^2-1A^3+0A^4+1A^5\)
\(\psi^4_{(t=0)}=\frac{\sqrt3}{2}A^1+\frac{\sqrt3}{2}A^2+0A^3+\frac{\sqrt3}{2}A^4-\frac{\sqrt3}{2}A^5\)
\(\psi^5_{(t=0)}=\frac{1}{2}A^1+\frac{\sqrt3}{2}A^2+1A^3-\frac{\sqrt3}{2}A^4+\frac{1}{2}A^5\)
Les conditions initiales de position pour chacune des masses permettent de résoudre ce système.
Par exemple : \(\psi^2=\psi^4\) et \(\psi^1=\psi^5\) (en \(t=0\))
\(\Rightarrow \psi^2-\psi^4=0\) et \(\psi^1-\psi^5=0\Rightarrow A^2=A^4=0\)
N'interviennent alors que les modes 1, 3, et 5 qui possèdent la même symétrie (symétrie par rapport à la médiatrice).
9- On suppose de plus que dans l'état initial toutes les masses ont la même amplitude initiale : \(\psi^1 = \psi^2 = \psi^3 = \psi^4 = \psi^5\) en \(t=0\).
Le système à résoudre est alors :
\(\psi^1_{(t=0)}=\frac{1}{2}A^1+A^3+\frac{1}{2}A^5=A\)
\(\psi^2_{(t=0)}=\frac{\sqrt3}{2}A^1-\frac{\sqrt3}{2}A^5=A\)
\(\psi^3_{(t=0)}=A^1-A^3+A^5=A\)
On pose \(\Delta=\left(\begin{array}{ccc} \frac{1}{2}&1&\frac{1}{2} \\ \frac{\sqrt3}{2}&0&-\frac{\sqrt3}{2} \\ 1&-1&1 \end{array} \right)\), et on retrouve : \(\textrm{d\'et }\Delta=-\frac{\sqrt3}{2}\)
On pose \(\Delta_A=\left(\begin{array}{ccc} A&1&\frac{1}{2} \\ A&0&-\frac{\sqrt3}{2} \\A&-1&1 \end{array} \right)\), et on trouve :
\(\textrm{d\'et }\Delta_A=A[(-\frac{\sqrt3}{2}-1)-(\frac{1}{2}+\frac{\sqrt3}{2})]\)
On obtient alors : \(A^1=-\frac{\textrm{d\'et }\Delta_A}{\textrm{d\'et }\Delta}=\frac{A}{3}(\sqrt3+2)\)
et de même : \(A^5=\frac{A}{3}(\sqrt3-2) et A^3=\frac{A}{3}\)
\(\psi(t)=\frac{A}{3}(\sqrt3+2)M_1\cos\omega_1t+\frac{A}{3}M_2\cos\omega_2t+ \frac{A}{3}(\sqrt3-2)\cos\omega_5t\)
où les vecteurs \(M_1\), \(M_2\) et \(M_5\) sont ceux calculés précédemment, et déterminent les amplitudes des 5 masses dans cette vibration.
Remarque :
Il est intéressant de comparer la valeur des coefficients qui interviennent dans le développement en exprimant leur valeur relative :

On peut remarquer que si les plombs de la corde plombée sont lâchés selon des positions alignées, la corde ne vibre pas selon une vibration périodique : pour que ce soit le cas, il faudrait que les modes propres qui interviennent dans le développement aient des périodes qui admettent un plus petit commun multiple (qui serait alors la période de la combinaison) En particulier, la vibration ne conservera pas l'alignement initial des plombs.
Par contre, ce sera le cas si l'on remplace la corde plombée par une corde vibrante possédant une densité de masse constante. On étudiera ce cas ultérieurement par la théorie des séries de Fourier.
Les différences entre ces 2 cas (corde plombée et corde continue) sont résumées ci-dessous :
Corde plombée
Nombre fini de degré de liberté
Fréquences dans des rapports non-nécessairement rationnels
Vibration non-périodique
Corde continue
Nombre infini de degré de liberté
Fréquences dans des rapports entiers
Fréquences multiples de celle du fondamental
Vibration périodique