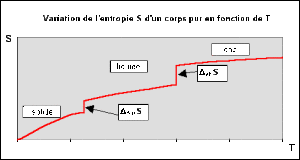
Variation de l'entropie avec la température

L'entropie[1] d'un corps pur est une fonction croissante de la température ; cette croissance est discontinue à chaque température correspondant à un changement d'état physique du corps pur. Le symbole de cette grandeur d'état est \(S\).

La dérivée de l'entropie par rapport à la température est \(\frac{\textrm dS}{\textrm dT} = \frac{C_p}{T}\) .

La variation d'entropie d'un corps pur ne possédant qu'une seule variété allotropique a donc l'allure de la courbe présentée ci-contre .

Il vient donc pour une mole[2] de solide pur dans son état standard[3] :

\(S_{\textrm{solide, }T}=\int_0^T\frac{C_{p, \textrm{solide}}}{T}\textrm dT\)

cela si le composé \(i\) reste à l'état solide dans l'intervalle de température de 0 à \(T\) K.

Si au contraire le composé \(i\) passe à l'état liquide à \(T_\textrm{fus}\textrm{ K}\) et bout à \(T_\textrm{eb}\textrm{ K}\), alors il vient :

\(S_T=\int_0^{T_\textrm{fus}}\frac{{C_p}_ \textrm{solide}}{T}\textrm dT+\Delta_\textrm{fus}{S_T}_ \textrm{fus}+\int_{T_\textrm{fus}}^{T_\textrm{eb}}\frac{{C_p}_\textrm{liquide}}{T}\textrm dT+\Delta_\textrm{eb}{S_T}_\textrm{eb}+\int_{T_\textrm{eb}}^T\frac{{C_p}_\textrm{gaz}}{T}\textrm dT\)

où \(\Delta_\textrm{fus}{S_T}_\textrm{fus}=\textrm{ entropie de fusion }= \frac{\Delta_\textrm{fus}{H_T}_\textrm{fus}}{T_\textrm{fus}}\)

et \(\Delta_\textrm{eb}{S_T}_\textrm{eb}=\textrm{ entropie d'ébullition }= \frac{\Delta_\textrm{eb}{H_T}_\textrm{eb}}{T_\textrm{eb}}\) .

L'animation ci-dessous illustre cette variation dans le cas de l'eau pure :