État d'équilibre pour une réaction entre gaz

Nous avons vu au paragraphe précédent que l'enthalpie libre d'un système dans lequel la transformation X à P se produit a pour expression :

\(G = ( 1-\xi ).( \mu^{\circ}_\textrm X + R.T \ln (a_\textrm X) ) + \xi . ( \mu^{\circ}_\textrm P + R.T \ln (a_\textrm P) )\)

Nous allons à présent étudier la variation de \(G\) en fonction de \(\xi\) suivant l'état physique de \(\textrm X\) et \(\textrm P\) et en tirer les conséquences quand à l'évolution du système .

Cas 1 : X et P sont des gaz parfaits. Transformation à pression constante p = 1 bar.

Pour un gaz parfait, l'activité est définie comme le rapport de sa pression partielle[1] à la pression de référence \(p^{\circ} = 1\textrm{ bar}\).

Nous avons donc \(a_\textrm X = \frac{p_\textrm X}{p^{\circ}} = \gamma_\textrm X . \frac{p_t}{p^{\circ}}\) où \(\gamma_\textrm X\) est la fraction molaire[2] de \(\textrm X\) dans le mélange gazeux et \(p_t\) la pression totale des gaz dans le mélange. Cette pression étant constante et égale à \(p^{\circ} = 1\textrm{ bar}\), il vient :

\(a_\textrm X = \gamma_\textrm X =\frac{n_\textrm X}{(n_\textrm X + n_\textrm P)} = \frac{(1 - \xi )}{1}\) et de même \(a_\textrm P = \frac{\xi}{1}\)

L'expression de \(G\) devient donc \(G = (1 - \xi).(\mu^{\circ}_\textrm X + R.T \ln (1 - \xi) ) + \xi . ( \mu^{\circ}_\textrm P + R.T \ln (\xi) )\)

soit \(G - \mu^{\circ}_\textrm X = \xi . \Delta_\textrm rG^{\circ} + (1 - \xi). R.T \ln (1 - \xi) + \xi . R.T \ln (\xi)\)

ou encore si \(T = 298 \textrm K\) : \(G - \mu^{\circ}_\textrm X = \Delta_\textrm rG^{\circ}. \xi + 2493 . ((1 - \xi). \ln (1 - \xi) + \gamma . \ln (\xi) )\)

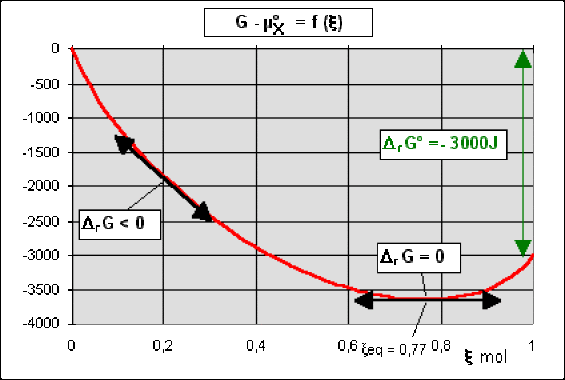
Dans le cas où \(\Delta_\textrm rG^{\circ}\) vaut - 3000 J.mol-1, la courbe ci-contre (en rouge) représente les variations de \(G - \mu^{\circ}_\textrm X\) en fonction de l'avancement \(\xi\) de la réaction \(\textrm{X (gaz)}\to \textrm{P (gaz)}\) . La pente de la tangente à cette courbe représente \(\Delta_\textrm rG\) puisque par définition \(\Delta_\textrm rG = \frac{\textrm dG}{\textrm d\xi}\) .

Lorsque \(\xi = 0\), \(\Delta_\textrm rG\) est négatif donc la réaction \(\textrm{X (gaz)}\) à \(\textrm{P (gaz)}\) va se produire et \(\xi\) va croître. Cette réaction va se poursuivre jusqu'à ce que \(G\) soit minimum, c'est à dire jusqu'à ce que \(\xi = \xi_\textrm{eq}\) et \(\Delta_\textrm rG = 0\).

\(\xi_\textrm{eq} = \textrm{0,77 mol}\) correspond donc à l'avancement de la réaction à l'équilibre, la composition du système étant alors de 0,77 mol de \(\textrm P\) et 0,23 mol de \(\textrm X\).

Notez bien sur ce graphique la différence qu'il y a entre \(G\) du système, \(\Delta_\textrm rG\) et \(\Delta_\textrm rG^{\circ}\).

Position de l'état d'équilibre suivant la valeur de ΔrG°

L'animation ci-dessous vous permet de faire varier l'enthalpie libre standard \(\Delta_\textrm rG^{\circ}\) de la réaction et de visualiser l'influence de cette variation sur la forme de la courbe \(G = f(\xi)\) . Elle vous permet également de constater l'influence de cette variation sur la position d'équilibre.

Conclusions

Lorsqu'une transformation du type \(\textrm X \to \textrm P\) se déroule dans un système à température constante, la transformation s’arrête lorsque l'avancement de réaction est tel que l'enthalpie libre du système atteint la valeur la plus faible possible.

Lorsque la transformation\( \textrm X \to \textrm P\) se produit en phase homogène, cette valeur de G correspond à un minimum, c'est à dire à la valeur de \(\xi = \xi_\textrm{eq}\) telle que \(\frac{\textrm dG}{\textrm d\xi} = \Delta_\textrm rG = 0\) .

La valeur de \(\xi_\textrm{eq}\) dépend de \(\Delta_\textrm rG^{\circ}\) : plus \(\Delta_\textrm rG^{\circ}\) est négative et plus la valeur de \(\xi_\textrm{eq}\) est proche de la valeur maximale qui correspond à un taux d'avancement de réaction de 100% . Au contraire, plus \(\Delta_\textrm rG^{\circ}\) est positive et plus \(\xi_\textrm{eq}\) est faible et proche de zéro.