État d'équilibre pour une réaction entre phases condensées
Nous avons vu précédemment que l'enthalpie libre d'un système dans lequel la transformation \(\textrm X \to \textrm P\) se produit a pour expression :
\(G = ( 1- \xi ).( \mu^{\circ}_\textrm X + R.T \ln (a_\textrm X) ) + \xi . ( \mu^{\circ}_\textrm P + R.T \ln (a_\textrm P) )\)
Nous allons à présent continuer d'étudier la variation de \(G\) en fonction de \(\xi\) suivant l'état physique de \(\textrm X\) et \(\textrm P\) et en tirer les conséquences quand à l'évolution du système .
Cas 2 : X et P sont des solides ou des liquides non miscibles.
Nous avons donc \(a_\textrm X = a_\textrm P = 1\), valeur indépendante de \(\xi\).
L'expression de \(G\) devient donc \(G = (1 - \xi).(\mu^{\circ}_\textrm X + R.T \ln (1) ) + \xi . ( \mu^{\circ}_\textrm P + R.T \ln (1) )\)
soit \(G - \mu^{\circ}_\textrm X = \xi . \Delta_\textrm rG^{\circ}\) .
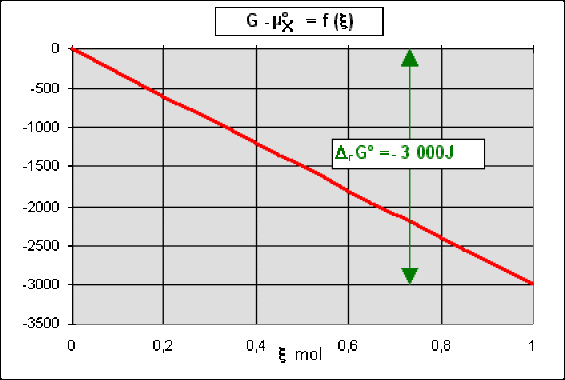
Reprenons, comme dans le paragraphe précédent le cas où \(\Delta_\textrm rG^{\circ} = - 3000\textrm{ J.mol}^{-1}\). Dans le cas d'une réaction \(\textrm X_\textrm{(solide)}\to \textrm P_\textrm{(solide)}\) l'enthalpie du système \(G\) ne fait que diminuer avec \(\xi\) et \(\Delta_\textrm rG = \Delta_\textrm rG^{\circ} < 0\) quel que soit \(\xi\) .
La réaction \(\textrm X_\textrm{(solide)}\to \textrm P_\textrm{(solide)}\) est donc totale , elle ne s'arrête qu'avec la disparition complète du réactif \(\textrm X\).
C'est la grande différence avec une réaction s'effectuant en phase homogène, un processus totalement hétérogène[2] sera soit total soit impossible suivant le signe de \(\Delta_\textrm rG^{\circ}\).
Position de l'état d'équilibre suivant la valeur de ξ
L'animation ci-dessous vous permet de faire varier l'enthalpie libre standard \(\Delta_\textrm rG^{\circ}\) de la réaction et de visualiser l'influence de cette variation sur la forme de la courbe \(G = f(\xi)\) . Elle vous permet également de constater l'influence de cette variation sur la position d'équilibre.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Conclusion
Lorsqu'une transformation du type \(\textrm X\to \textrm P\) se déroule dans un système à température constante, la transformation s’arrête lorsque l'avancement de réaction est tel que l'enthalpie libre du système atteint la valeur la plus faible possible.
Lorsque la transformation \(\textrm X\to \textrm P\) se produit en phase homogène, cette valeur due G correspond à un minimum, c'est à dire à la valeur de \(\xi = \xi_\textrm{eq} telle que \frac{\textrm dG}{\textrm d\xi} = \Delta_\textrm rG = 0\) . La valeur de \(\xi_\textrm{eq}\) dépend de \(\Delta_\textrm rG^{\circ} : plus \Delta_\textrm rG^{\circ}\) est négative et plus la valeur de \(\xi_\textrm{eq}\) est proche de la valeur maximale . Au contraire, plus \(\Delta_\textrm rG^{\circ}\) est positive et plus \(\xi_\textrm{eq}\) est faible .
Lorsque la transformation se produit entre deux solides ou un solide et un liquide , alors cette valeur minimale de G correspond à \(\xi = \xi_\textrm{max}\) si \(\Delta_\textrm rG^{\circ}\) est négative où à \(\xi = 0 si \Delta_\textrm rG^{\circ}\) est positive. Pour une réaction de ce type, ou bien la réaction est totale, ou bien elle ne se fait pas du tout ! La fusion de la glace est un exemple d'une telle transformation : à une température inférieure à 0°C, \(\Delta_\textrm rG^{\circ}\) est positive et donc on ne peut pas avoir d'eau liquide coexistant avec la glace en dessous de 0°C, de même, à une température supérieure à 0°C, \(\Delta_\textrm rG^{\circ}\) est négative et un glaçon placé à une température de 20°C fond totalement.