Association mixte (1)
Partie
Question
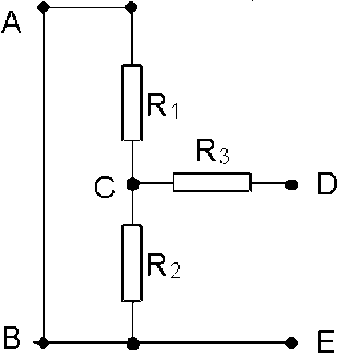
Calculer la résistance équivalente au réseau ci-dessous vu de \(D\) et \(E\).
Application numérique : \(R_1= 470 \;\Omega\), \(R_2 = 1000\;\Omega\), \(R_3 = 3300\;\Omega\)
Aide simple
Redessiner le réseau en supprimant les points qui ne sont ni des noeuds, ni des bornes.
Aide détaillée
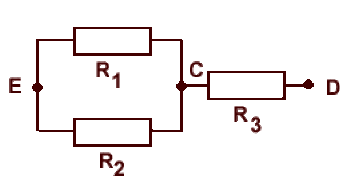
Les trois dipôles sont reliés au noeud \(C\) et à une des bornes \(D\) ou \(E\) ; on peut redessiner le réseau comme suit :
Solution simple
\(R_{DE}=3382,5\;\Omega\)
Solution détaillée
Entre \(\displaystyle {E \textrm{ et } C, R_1 \textrm{ et }R_2}\) sont en parallèles : les conductances s'additionnent.
\(\displaystyle{G_{EC}=G_1+G_2}\)
\(\displaystyle{\frac{1}{R_{EC}}=\frac{1}{R_1}+\frac{1}{R_2}}\)
\(\displaystyle{R_{EC}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}}=\frac{1}{\frac{1}{470}+\frac{1}{1000}}=82,5\;\Omega}\)
Cet ensemble est en série avec \(R_3\) : les résistances s'additionnent.
\(\displaystyle{\begin{array}{lll}R_{ED} & = & R_{EC}+R_{CD}=R_{EC}+R_{3}\\ & = & 82,5+3300=3382,5 \Omega\end{array}}\)