Association mixte (2)
Partie
Question
Question 1
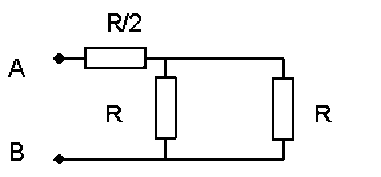
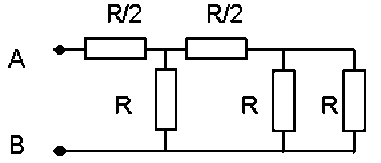
Calculer la résistance équivalente aux réseaux ci-dessous, vus de \(\displaystyle{A \textrm{ et } B}\)
Question 2
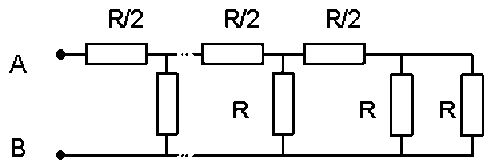
En déduire sans calcul la résistance entre \(A\) et \(B\) de la ligne de transmission ci-contre, formée d'un nombre infini de cellules identiques.
On enlève une cellule de la ligne. Quelle est l'effet sur l'intensité du courant entrant en \(A\) dans la ligne ?
Aide simple
Utiliser la méthodologie d'étude des associations mixtes.
Aide détaillée
Identifier les nœuds du réseau ; calculer la résistance équivalente à la portion de réseau situé entre deux nœuds ou un nœud et une borne. Penser à utiliser le résultat des questions précédentes.
Solution simple
\(\displaystyle{R_{AB}=R}\) pour les trois réseaux.
L'intensité du courant entrant en \(A\) dans la ligne est indépendante du nombre de cellules.
Solution détaillée
Le premier réseau comporte un noeud \(C\)
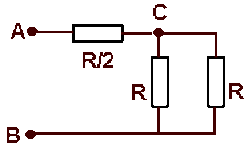
Entre \(\displaystyle{C \textrm{ et }B}\), on a deux dipôles de résistance \(R\) en parallèle : \(\displaystyle{R_{CB}=R/2}\).
Entre \(\displaystyle{A \textrm{ et } B}\), l'ensemble ci-dessus est en série avec un dipôle de résistance \(\displaystyle{R/2 : R_{AB}=R_{AC}+R_{CB}=R}\)
Le deuxième réseau comporte deux noeuds \(\displaystyle{C \textrm{ et }D}\).
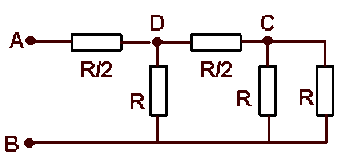
Entre \(\displaystyle{C \textrm{ et }B}\), ce réseau est identique au premier : \(\displaystyle{R_{CB}=R/2}\).
Entre \(\displaystyle{D \textrm{ et }B}\), ce réseau comporte deux ensembles en parallèle :
un dipôle de résistance \(R\)
un ensemble de trois dipôles, identique au premier réseau vu de \(\displaystyle{A \textrm{ et }B}\), donc de résistance équivalente égale à \(R\) d'où \(R_{DB}=R/2\).
Entre \(\displaystyle{A \textrm{ et }B, R_{AB}=R_{AD}+R_{DB}=R}\)
Question 2
Pour le troisième réseau, en remplaçant de proche en proche à partir de la droite les dipôles par leur résistance équivalente, on aboutit au même résultat.
Quelque soit le nombre de cellules, \(\displaystyle{R_{AB}=R}\), donc l'intensité du courant entrant en \(A\) ne change pas :
\(\displaystyle{I=\frac{U}{R_{AB}}=\textrm{cste}}\)