Application du théorème de Kennelly
Partie
Question
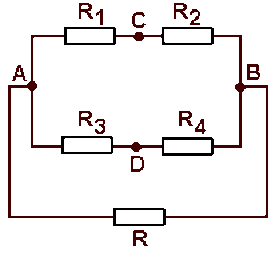
Ce réseau représente les élément passifs d'un pont de Wheatstone, dans le cas où la résistance interne de l'alimentation n'est pas négligeable.
Calculer la résistance équivalente au réseau :
a) vu de \(A\) et \(B\)
b) vu de \(C\) et \(D\)
Application numérique:\( \displaystyle{R_1=R_2=R_3=R_4=350\; \Omega; R = 50 \;\Omega}\)
Aide simple
Coup de pouce :
a) Faire la somme des conductances.
b) Redessiner le réseau.
Aide détaillée
Plus d'aide :
a)Faire l'inventaire des branches reliant \(A\) à \(B.\)
Remplacer les associations en série par leur résistance équivalente.
Faire la somme des conductances.
b)
Redessiner le réseau en cherchant les chemins permettant d'aller de \(C\) à \(D.\)
Utiliser le théorème de Kennelly pour transformer un triangle en étoile.
Utiliser les lois d'association en série et en parallèle.
Solution simple
a) \(R_{AB} = 43,75\;\Omega\)
b) \(R_C = 163,3\;\Omega\)
Solution détaillée
a) Trois branches relient \(A\) à \(B\) :
une branche contenant deux dipôles de résistance \(R_1\) et \(R_2\), en série.
une branche contenant deux autres dipôles de résistances\( R_3\) et \(R_4\), en série.
une branche contenant un dipôle de résistance\( R\).
la première branche a pour résistance équivalente
\(R_{12}=R_1+R_2=700 \;\Omega\)
la deuxième branche a pour résistance équivalente
\(R_{34}=R_3+R_4=700\;\Omega\)
les conductances s'ajoutent :
\(G_{AB}=G_{12}+G_{34}+G\)
\(\displaystyle{\frac{1}{R_{AB}}=\frac{1}{R_{12}}+\frac{1}{R_{34}}+\frac{1}{R}=\frac{1}{700}+\frac{1}{700}+\frac{1}{50}}\)
\(R_{AB} = 43,75\)
b) Pour aller de \(C\) à \(D,\) on peut passer soit par \(A\) soit par \(B\) ; \(A\) et \(B\) sont reliés par une branche contenant un dipôle de résistance \(R.\) On peut redessiner le réseau comme suit :
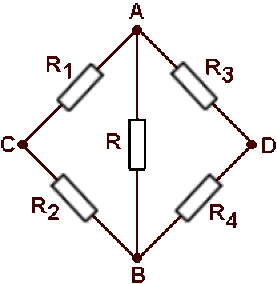
Pour calculer la résistance du réseau vu de \(C\) et \(D,\) on transforme un des triangles en étoile, par exemple \(ABC\)
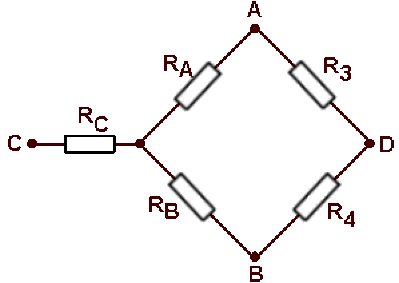
d'après le théorème de Kennelly.
\(R_{C} = \frac{R_{1}R_{2}}{R_{1}+R_{2}+R} = \mathrm{163,3} ~\Omega\)
\(R_{B} = \frac{RR_{2}}{R_{1}+R_{2}+R} = \mathrm{23,3} ~\Omega\)
\(R_{A} = \frac{RR_{1}}{R_{1}+R_{2}+R} = \mathrm{23,3} ~\Omega\)
On remplace les dipôles en série par leur résistance équivalente
\(R_{A3} = R_{A} + R_{3} = \mathrm{373,3} ~\Omega\)
\(R_{B4} = R_{B} + R_{4} = \mathrm{373,3} ~\Omega\)
\(C_{A3B4} = C_{A3} + C_{B4}\)
\(\frac{1}{R_{A3B4}} = \frac{1}{R_{A3}} + \frac{1}{R_{B4}}\)
\(R_{A3B4} = \mathrm{186,7}~\Omega\)
et on applique la loi d'association en série.
\(R_{CD} = R_{C} + R_{A3B4} = \mathrm{350} ~\Omega\)