Pont de Wheatstone
Partie
Question
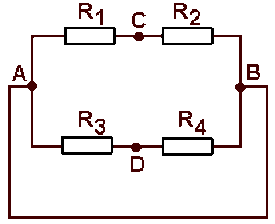
Ce réseau représente les éléments passifs d'un pont de Wheatstone. Calculer la résistance équivalente au réseau :
Question 1 : vu de \(\displaystyle{A \textrm{ et }B}\)
Question 2 : vu de \(\displaystyle{C \textrm{ et }D}\)
Application numérique :
\(\displaystyle{R_1=R_2=R_3=R_4=350\;\Omega}\)
Aide simple
Coup de pouce :
Question 1: Faire la somme des conductances.
Question 2 : Deux points d'un réseau sont équivalents s'ils sont reliés par un fil de connexion.
Aide détaillée
Plus d'aide :
Question 1 :Ne pas oublier le fil de connexion reliant \(\displaystyle{A \textrm{ et }B}\).
Question 2 : Redessiner le réseau en cherchant les chemins possibles pour aller de \(\displaystyle{C \textrm{ à }D}\).
Solution simple
1) \(\displaystyle{R_{AB}=0}\)
2) \(\displaystyle{R_{CD}=350\;\Omega}\)
Solution détaillée
Question 1
Entre \(\displaystyle{A ~\textrm{et}~ B}\) se trouvent trois branches associées en parallèle :
une branche contenant deux dipôles associés en série, de résistance \(\displaystyle{R_1 \textrm{ et }R_2}\).
une branche contenant deux autres dipôles associés en série, deux résistances \(R_3\) et \(R_4.\)
un fil de connexion.
La conductance de l'ensemble est égale à la somme des conductances.
La conductance d'un fil de connexion est infinie.
Donc la conductance de l'ensemble est infinie, et la résistance de ce réseau, vu de \(\displaystyle{A \textrm{ et }B}\), est nulle.
Question 2
Les points \(\displaystyle{A \textrm{ et }B}\) reliés par un fil de connexion, sont électriquement équivalents. Pour aller de \(\displaystyle{C \textrm{ à }D}\), on peut suivre le chemin \(R_2, B , R_4\), ou le chemin \(R_1, A,R_3;\) comme \(A ~\textrm{et}~ B\) sont équivalents, on peut redessiner le réseau comme suit :
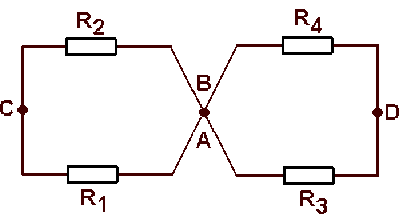
on remplace les dipôles en parallèle par leur résistance équivalente ; pour \(\displaystyle{R_1 \textrm{ et }R_2}\) :
\(\displaystyle{G_{12}=G_1+G_2}\)
\(\displaystyle{\frac{1}{R_{12}}=\frac{1}{R_1}+\frac{1}{R_2}}\)
\(\displaystyle{R_{12}=175\;\Omega}\)
pour \(\displaystyle{R_3 \textrm{ et }R_4}\) :
\(\displaystyle{G_{34}=G_3+G_4}\)
\(\displaystyle{\frac{1}{R_{34}}=\frac{1}{R_3}+\frac{1}{R_4}}\)
\(\displaystyle{R_{34}=175\;\Omega}\)
vu de \(\displaystyle{C \textrm{ et }D}\), ce réseau a donc pour résistance \(\displaystyle{R_{CD}=R_{12}+R_{34}=350\;\Omega}\)
\(\displaystyle{R_B=\frac{RR_2}{R_1+R_2+R}=23,3\;\Omega}\)
\(\displaystyle{R_A=\frac{RR_1}{R_1+R_2+R}=23,3\;\Omega}\)
On remplace les dipôles en série par leur résistance équivalente
\(\displaystyle{ R_{A3}=R_A+R_3=373,3\;\Omega}\)
\(\displaystyle{R_{B4}=R_B+R_4=373,3\;\Omega }\)
On remplace les dipôles en parallèle par leur résistance équivalente
\(\displaystyle{G_{A3B4}=G_{A3}+G_{B4}}\)
\(\displaystyle{\frac{1}{R_{A3B4}}=\frac{1}{R_{A3}}+\frac{1}{R_{B4}}}\)
\(\displaystyle{R_{A3B4}=186,7\;\Omega}\)
et on applique la loi d'association en série.
\(\displaystyle{R_{CD}=R_C+R_{A3B4} =350\;\Omega}\)