Diviseur de courant
Partie
Question
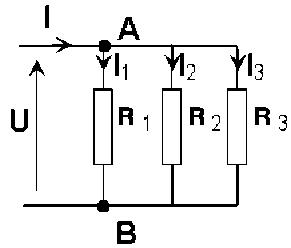
Quelle est l'intensité du courant dans la branche 2 du circuit ci-contre ?
Application numérique :
\(\displaystyle{I=150\textrm{ mA}}\)
\(\displaystyle{R_1=470\;\Omega}\)
\(\displaystyle{R_2=1000\;\Omega}\)
\(\displaystyle{R_3=3300\;\Omega}\)
Aide simple
Dans une association en parallèle, les conductances des dipôles s'additionnent.
Aide détaillée
Calculer la conductance de l 'association
Utiliser la relation caractérisant le diviseur de courant.
Solution simple
\(\displaystyle{I_2=43,7\textrm{ mA}}\)
Solution détaillée
La conductance de l'association en parallèle de bornes \(\displaystyle {A \textrm{ et } B}\) est égale à la somme des conductances des trois dipôles associés
\(\displaystyle{\begin{array} {lll}G_{AB} & = & G_1+G_2+G_3\\& = & 1/R_1+1/R_2+1/R_3=3.43\textrm{ mS}\end{array}}\)
Dans chaque dipôle, l'intensité est proportionnelle à la conductance ; donc dans la branche 2 :
\(\displaystyle{I_2=I\frac{G_2}{G_{AB}}=\frac{I}{R_2G_{AB}}=43,7\textrm{ mA}}\)