Association de générateurs en parallèle
Partie
Question
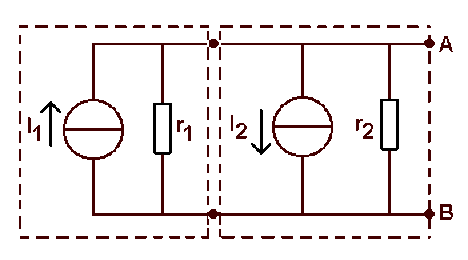
Quelles sont les caractéristiques des générateurs équivalents à l'association ci-contre?
Application numérique : \(\displaystyle{I_1 = 10 \textrm{ mA}, I_2 = 3 \textrm{ mA} ; r_1 = r_2 = 50 \;\Omega}\)
Aide simple
Tenir compte du sens des courants de court-circuit.
Aide détaillée
Déterminer le générateur de Norton équivalent à l'association ; en déduire les caractéristiques du générateur de Thévenin.
Solution simple
Modèle de Norton : \(I_0 = 7 \textrm{ mA}, g = 40 \textrm{ mS}\)
Modèle de Thévenin : \(E = 175 \textrm{ mV}, r = 25\;\Omega\)
Solution détaillée
a) modèle de Norton
Dans une association en parallèle, le courant de court-circuit du générateur équivalent est égal à la somme algébrique des courants de court-circuit, et la conductance interne à la somme des conductances.
\(\left.\begin{array}{l}I_1\textrm{ et }I_2 \textrm{ sont de sens diff\'erent}\\I_1> I_2\end{array}\right \}I_0=I_1-I_2=7\textrm{ mA}\)
\(g = g_1 + g_2 = 1/50 +1/50 = 4.10^{- 2}\textrm{ S}\)
d'où le schéma :

b) modèle de Thévenin :
La f.é.m. est égale à la tension à vide :
\(\displaystyle{E=\frac{I_0}{g}=\frac{7.10^{-3}}{4.10^{-2}}=0,175\textrm{ V}}\)
La résistance interne est l'inverse de la conductance :
\(\displaystyle{r=\frac{1}{g}=\frac{1}{4.10^{-2}}=25\;\Omega}\)