Champ uniforme
Partie
Question
Champ uniforme (*)
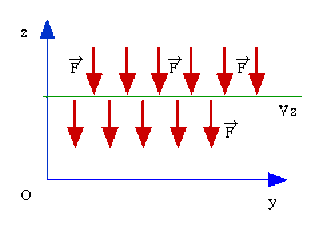
Soit le champ uniforme représenté sur la figure et tel que\( \displaystyle{\overrightarrow F=-F_0\overrightarrow k}\) dirigé suivant les \(z\) négatifs.
1/ Montrer que ce champ dérive d'un potentiel.
2/ Calculer ce potentiel.
3/ En déduire l'énergie potentielle d'un point matériel de masse m placé dans un champ de pesanteur uniforme
Aide simple
Le gradient se réduit à une seule composante verticale
Solution détaillée
1/ La seule composante non nulle de \(\overrightarrow F\) est dirigée suivant Oz et elle ne dépend pas de \(x,y, \textrm{ ou }z\), ce qui implique que \(\overrightarrow{Rot}\quad\overrightarrow F=\overrightarrow0\).
2/ \(\displaystyle{\overrightarrow F=-\textrm{grad }\overrightarrow U=-\frac{\textrm dU}{\textrm dz}\overrightarrow k ;F_0=\frac{\textrm dU}{\textrm dz}}\) ;
donc \(U = F_0 z + \textrm{Constante}\).
Si \(U = 0 \textrm{ pour }z = 0, \textrm{ alors }U =F_0 z\)
Pour\( z = z_0, \textrm{ alors }U = F_0 (z-z_0 )\).
3/ Ici \(\overrightarrow F=-mg\overrightarrow k\) ; \(F_0 = mg \textrm{ et }U_m = mg (z-z_0)\)